prosta
denatlu: y=−x+3. S(1,2), d=2√2. Jak mogę znaleźć punkt na tej prostej w oddali od punktu S o d=2√2?
25 kwi 21:27
Eta:
P(x, −x+3) , S(1,2) |PS|= 2√2 ⇒ |PS|2= 8
(x−1)2+(2+x−3)2=8
(x−1)2+(x−1)2=8
2(x−1)2=8
(x−1)2=4 ⇒ x−1=2 v x−1 =−2
dokończ ...... P(3,0) , P(−1,4)
25 kwi 21:43
irena_1:
rozwiązać układ równań:
(x−1)2+(y−2)2=(2√2)2
y=x−3
czyli znaleźć punkty wspólne okręgu o środku S i promieniu d oraz danej prostej
25 kwi 21:44
denatlu: a wektorami dałoby radę?
25 kwi 21:47
denatlu:
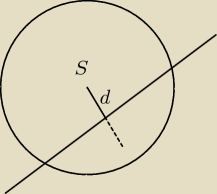
dobra ja coś źle tutaj robie. Jest okrę sobie (x−1)
2+(y−2)
2=16 i prosta y=x−3. Mam znaleźć
równanie okręgu symetrycznego względem tej prostej
sam.
Żaden z tych puntów nawet nie jest naszym środkiem, to źle
25 kwi 22:02
Eta:
Echh

Zamiast napisać całą treść zadania , to wymyślasz "skróty" !
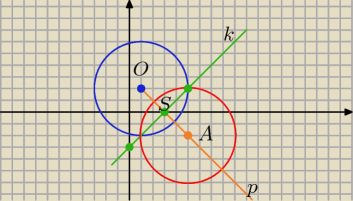
O(1,2) prosta p⊥k to: p: y= −(x−1)+2 ⇒ p: y= −x+3
Punkt wspólny S prostych k i p {y=x−3
{y=−x+3 to S(3,0)
→ →
OS= SA ⇒[2,−2]= [x−3,y] ⇒ x=5, y=−2 A(5,−2) −− środek okręgu symetrycznego i r=4
o : (x−5)
2+(y+2)
2=16
25 kwi 22:48
 dobra ja coś źle tutaj robie. Jest okrę sobie (x−1)2+(y−2)2=16 i prosta y=x−3. Mam znaleźć
równanie okręgu symetrycznego względem tej prostej sam.
Żaden z tych puntów nawet nie jest naszym środkiem, to źle
dobra ja coś źle tutaj robie. Jest okrę sobie (x−1)2+(y−2)2=16 i prosta y=x−3. Mam znaleźć
równanie okręgu symetrycznego względem tej prostej sam.
Żaden z tych puntów nawet nie jest naszym środkiem, to źle
 Echh
Echh Zamiast napisać całą treść zadania , to wymyślasz "skróty" !
O(1,2) prosta p⊥k to: p: y= −(x−1)+2 ⇒ p: y= −x+3
Punkt wspólny S prostych k i p {y=x−3
{y=−x+3 to S(3,0)
→ →
OS= SA ⇒[2,−2]= [x−3,y] ⇒ x=5, y=−2 A(5,−2) −− środek okręgu symetrycznego i r=4
o : (x−5)2+(y+2)2=16
Zamiast napisać całą treść zadania , to wymyślasz "skróty" !
O(1,2) prosta p⊥k to: p: y= −(x−1)+2 ⇒ p: y= −x+3
Punkt wspólny S prostych k i p {y=x−3
{y=−x+3 to S(3,0)
→ →
OS= SA ⇒[2,−2]= [x−3,y] ⇒ x=5, y=−2 A(5,−2) −− środek okręgu symetrycznego i r=4
o : (x−5)2+(y+2)2=16