problem z calka, polem sprd: Witam! Mam obliczyc pole ograniczone krzywymi: y² = 4x, y = 2x−4. Jak sobie to narysuję to widzę, że nie da się liczyc po x., więc wyznaczami x z jednegi i drugieg i całkuje po y z granicami od −2 do 4. Oczywiscie odejmuje od funkcji ograniczajacej z góry funkcje poniżej. Cały czas dostaje wynik −9. a ma byc 9. Czemu? Jezeli ktos bylby w stanie pomoc. Moja calka wyglada tak: ∫(−2,4) (y²/4 − y/2 + 2)dy

sprd: −2 a nie 2 w ostatnim wyrazie ma byc.

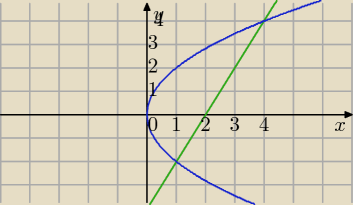
Mila: Punkty przecięcia: y²=4x y=2x−4 (2x−4)²=4x 4x²−16x+16=4x 4x²−20x+16=0 Δ=400−4*16*4=400−256=144

	20−12		20+12
x1=		=1 lub x=		=4
	8		8

y₁=−2√1=−2 lub y=2√4=4 obszar normalny względem OY

	y2
x=
	4

2x=y+4

	1
x=		y+2
	2

	1		y2
P=−2∫4(		y+2−		)dy= dokończ ( wynik 9 )
	2		4

sprd: MIla, i mój problem pojawia się chyba w ostaniej fazie tego zadanka. Dochodze do samego momentu liczenia calki oznaczone, z tym ze licze y²/4 − 1/2y − 2 a Ty masz inne znaki. Uczylem sie, ze zawsze od funkcji ograniczajacej z gory odejmuje funkcje ograniczajaca z dolu i dla pól liczonych po iksie dziala. A tu jest inaczej, czyli tak naprawde jak? Zawsze jak licze po igreku jest inna kolejnosc?

Mila: Jak inaczej, odwróć układ, abyś miał dodatnią półoś Ox u góry. Od funkcji liniowej odejmujesz kwadratową.