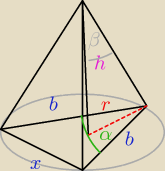
stereometria kiełbasa 514 Alois~: Podstawą ostrosłupa jest trójkąt równoramienny, w którym boki równe mają długość b, a kąt między nimi zawarty jest równy α. Oblicz objętość ostrosłupa, jeśli każda krawędź boczna tworzy z wysokością ostrosłupa kąt β wszystko sobie policzyłam i wychodzi mi

b3 √2−cosα		√2		√1−cosα
	a w odpowiedzi jest...		b3
12tgβ		12		tgβ

i się zastanawiam czy to ja popełniłam bład i jaki czy może ktoś mi pokazać w którym momencie skopałam P_p = 1/2 b² sinα x²=2b² − 2b² cosα => x=b √2−cosα potem wyliczam R

b √2−cosα
	= 2R
sinα

	b √2−cosα
R=
	2sinα

R		R		b √2−cosα
	= tgβ => H=		=> H=
H		tgβ		2sinα tgβ

i ta objetość którą podałam juz na poczatku..

Dominik: x = b√2(1 − cosα) dalej reszta ok i odpowiedz bedzie sie zgadzala.

Alois~: o faktycznie dzięki Dominik jak tam przygotowania ?

Dominik: strasznie powoli; robie dziennie po 10 zadan, bo wiecej mi sie juz po prostu nie chce. chce miec to juz za soba.

Alois~: zauważyłam że sporo osób im blizej tym mniej robi.