algebra dawid: Trivial mógłbyś zajrzeć tu? Wykaż, że A ∩ B jest podprzestrzenią V oraz pokaż, że: dim(A+B)=dim(A)+dim(B)−dim(A∩B). Wiemy, że A i B są skończenie wymiarowymi podprzestrzeniami V.

Trivial: Te zadania są wszystkie takie same... Mógłbyś się trochę wysilić.

dawid: Ale, że z definicji ?

Trivial: Dwa warunki: 1. Suma dwóch wektorów z U pozostaje w U. 2. Wektor z U pomnożony przez skalar również jest w U.

dawid: Znaczy mówimy wpierw o dowodzeniu A ∩ B, to czy nie powinniśmy wykorzystać wiedzy, że A i B są skończenie wymiarowymi podprzestrzeniami V ? Bo cały czas szukam co to dokładnie znaczy − w sensie definicji.

Trivial: To że są to skończenie wymiarowe przestrzenie liniowe oznacza tyle, że można je przedstawić w postaci wektorów. Czyli np może być że V = R³ albo coś podobnego.

dawid: ok, to wpierw A ∩ B, tylko jak to wykorzystać wiem, że można to rozpisać: <v₁, v₂> e A ∩ B ⇔ v₁ ∊ A ∧ v₂ ∊ B To może się jakoś przydać ?

Trivial: Zobacz czy warunki z (19:24) działają dla U = A∩B.

dawid: To wiem, ale chodziło mi o coś innego: ∀v₁, v_{2∊ U} v₁ + v₂ ∊ U i chodziło mi o to, czy te wektory podstawić pod to co wyżej rozpisałem, czy dało by tak radę ?

dawid: Skoro U = A ∩ B to czy możemy zapisać: v₁ + v₂ ∊ U v₁ + v₂ ∊ A ∩ B (v₁ + v₂) ⇒ A ∩ B (v₁ + v₂) ⇒ <v₁, v₂> ∊ A ∩ B (v₁ + v₂) ⇒ v₁ ∊ A ∧ v₂∊B ale pewnie to bez sensu

Trivial: Rozwiązanie ma być dla dowolnych wektorów (a nie tylko dwuwymiarowych). Niech u ∊ A∩B ⇔ u ∊ A ⋀ u ∊ B oraz v ∊ A∩B ⇔ v ∊ A ⋀ v ∊ B. 1. u+v ∊ A∩B ⇔ u+v ∊ A ⋀ u+v ∊ B. Skoro u oraz v należą do A, to u+v również należy do A (definicja przestrzeni liniowej). Analogicznie dla B. A zatem u+v należy do A oraz B. OK 2. αu ∊ A∩B ⇔ αu ∊ A ⋀ αu ∊ B. Tak samo jak punkt 1...

dawid: αu ∊ A ∩ B ⇔ αu ∊ A ∧ αu ∊ B Jeżeli u należy do A, to αu też należy do A oraz jeżeli u należy do B, to także αu należy do B. Więc αu należą do A i B. tak ?

Trivial: Tak. I to wystarczy, żeby αu należało do A∩B.

dawid: Takie to proste było, brakuje mi obycia w dowodach. A jak zrobić to z tym dimem? Bo tego jeszcze nie miałem na wykładzie, a chciałbym poznać co to znaczy (tj.: czytałem o tym − gdzieś było napisane, że jest to moc dowolnej bazy przestrzeni liniowej). Ale chciałbym widzieć jak to zrobić.

Trivial: dim(A) to wymiar przestrzeni A. Jest to minimalna ilość wektorów bazowych, które rozpinają tę przestrzeń. Przykład 1 R³ to przestrzeń wszystkich wektorów trójwymiarowych. Żeby ją opisać trzeba użyć przynajmniej 3 wektorów − np. (1,0,0), (0,1,0), (0,0,1). Wtedy każdy inny wektor możemy opisać jako kombinację liniową tych 3 wektorów. (3,2,1) = 3*(1,0,0) + 2*(0,1,0) + 1*(0,0,1). podsumowując, dim(R³) = 3. Przykład 2 Weźmy wektory R³ leżące na płaszczyźnie opisanej równaniem x+y+z = 0. 1. Czy te wektory tworzą podprzestrzeń? 2. Jakie wektory tworzą bazę tej przestrzeni? 3. Jaki jest jej wymiar?

dawid: A co znaczy "rozpinają tę przestrzeń" − może pytania wydają się śmieszne, ale chcę dobrze zrozumieć ten materiał i zagadnienia z nim związane. A te podpunkty w przykładzie 2 to dla mnie? 1) Trzeba sprawdzać to z definicji, czy jest jakiś szybszy sposób ?

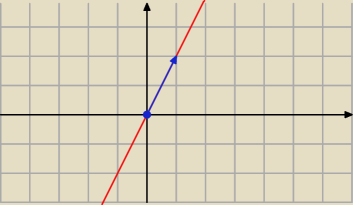
Trivial: Wektory rozpinają przestrzeń kiedy każdy element tej przestrzeni można opisać jako kombinację liniową tych wektorów.

	1 2		1 0
Powiedzmy, że mamy wektory		oraz		. Wektory te rozpinają przestrzeń

	1 2		1 0
U = { c*		+ d*		| c,d ∊ R }

	5 4
Czyli np. wektor		∊ U, gdyż możemy dobrać c = 2 oraz d = 1. Okazuje się, że U = R2,

	1 0		0 1
gdyż możemy wziąć wektory		(c = 0, d = 1) oraz		(c = 0.5, d = −0.5), które

rozpinają przestrzeń R² i należą one do U. Wymiar tej przestrzeni to 2 (dim(R²) = 2).

	1 2		2 4
Tym razem weźmy wektory		oraz		. Jaką przestrzeń rozpinają?

	1 2		2 4
U = { c*		+ d*		| c,d ∊ R }

Ale tak naprawdę wektory te nie są "niezależne". Jeden z nich możemy otrzymać mnożąc drugi z

	2 4		1 2
nich przez liczbę:		= 2*		, czyli U nie będzie już całym R2, ale pewnym wycinkiem

R² (prostą przechodzącą przez środek układu współrzędnych).

	1 2
U = { c*		| c ∊ R }

	1 2
U możemy opisać używając tylko jednego wektora bazowego:		, a zatem jej wymiar to 1.

Trivial: Te pytania są dla Ciebie, a w pierwszym wystarczy jeśli uzasadnisz dlaczego tak jest.

dawid: Weźmy wektory R³ leżące na płaszczyźnie opisanej równaniem x + y + z = 0. Odnośnie pytań: 1. Czy te wektory tworzą podprzestrzeń? 2. Jakie wektory tworzą bazę tej przestrzeni? 3. Jaki jest jej wymiar? Ad 1. Troszkę się pogubiłem w definicjach, ale czy nie wystarczy sprawdzić, czy nie są liniowo zależne? Czyli α₁x + α₂y + α₃z = 0, a skoro to równa się 0 więc, są liniowo niezależne więc tworzą podprzestrzeń ?

dawid: mam pytanie odnośnie przykładu z wektorami:

	2 1		1 0
napisałeś		i		i przykład: c = 2, d = 1

	5 4
2*(2, 1) + 1 * (1, 0) = (4, 2) + (1, 0) = (5, 2), a ty napisałeś		gdzie jest mój błąd ?

dawid: I dlaczego wymiar tej przestrzeni z przykładu z wykresem wynosi 2(dim(R²)) = 2 mógłbyś to jakoś uzasadnić ?

Trivial:

	1 2		1 0
Wykres jest dla przykładu drugiego, a błąd jest w tym że mamy wektory		,		, a nie

	2 1		1 0
		i		.

Odnośnie wcześniejszego: Nie taka jest definicja liniowej niezależności, a poza tym tutaj nigdzie jeszcze nie ma wektorów. Tutaj masz obrazek: http://www.wolframalpha.com/input/?i=plot+x%2By%2Bz+%3D+0 Przy pytaniu 1 chodzi mi o sławne 2 warunki. 1. Czy sumując dowolne dwa wektory z U dalej będziemy w U? 2. Czy mnożąc dowolny wektor z U dalej lądujemy w U? Po pierwsze, trzeba zauważyć, że wektor (0,0,0) spełnia równanie, a zatem jest szansa, że wektory leżące na tej płaszczyźnie tworzą podprzestrzeń. Jeśli by to nie zachodziło od razu odrzucamy kandydata. Wynika to z warunku drugiego u∊U ⇒ αu∊U dla α=0. Lekka odpowiedź: Płaszczyzna w R³ z zerem tworzy swój własny płaski świat. Wyobraźmy sobie nieskończony stół. Po stole chodzą mrówki, które mogą poruszać się tylko w 4 kierunkach. Nie mogą skakać do góry. Wektory mogą symbolizować ich kierunek ruchu. Jeżeli zero nie należałoby do płaszczyzny to niektóre wektory wskazywałyby kierunek do góry. Wtedy można byłoby łatwo wypaść ze stołu. Jeśli nie możemy wypaść to mamy przestrzeń.

Trivial: A wymiar jest 2 gdyż taka jest definicja wymiaru. "Jest to minimalna ilość wektorów bazowych, które rozpinają tę przestrzeń." Czyli jeśli mamy przestrzeń R², to kombinacje jednego wektora nie wystarczy żeby ją całą opisać. Kombinacje dwóch wektorów wystarczą. Kombinacje trzech wektorów są zbędne, gdyż ten trzeci sam jest kombinacją dwóch pozostałych. Np.

	1 0		0 2
1. c*		← nie da się tym opisać np. punktu		dla żadnego c

	1 0		0 1		c d
2. c*		+ d*		← można opisać każdy punkt		, czyli całe R2

	1 0		0 1		1 3		1 3
3. c*		+ d*		+ e*		← wektor		jest zbędny, można go utworzyć z

pozostałych:

	1 3		1 0		0 1
		= 1*		+ 3*

Czyli wymiar R² to 2.

Trivial: A z tym wektorem 21:43 to rzeczywiście masz rację. Mamy wektory bazowe:

	1 2		1 0		5 4
		oraz		kombinacja c,d która tworzy wektor		to

	5 4		1 2		1 0
		= 2*		+ 3*		(c = 2, d = 3)

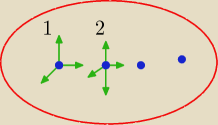
dawid: Łatwiej byłoby odpowiedzieć gdybyśmy operowali na układzie dwuwymiarowym, a nie trzywymiarowym. Łatwiej sobie to wyobrazić , a ta "lekka odpowiedź" to właśnie do tych dwóch podpunktów − wyżej napisanych ? Mrówki − mogą poruszać się tylko w 4 kierunkach, a dlaczego nie w trzech skoro operujemy na płaszczyźnie w R³ ? Mrówki przecież mogą poruszać się w nieskończenie wielu kierunkach przecież. Aby wykorzystać wskazówkę, trzeba ją wpierw zrozumieć

dawid: Ok, to jeżeli jesteśmy przy wektorach rozpinających mam jeden przykład którego z nich nie rozumiem, mianowicie: muszę określić wymiar przestrzeni rozpinajacej dla przykładu: (1, 0, 1, 0), (−1, 2, 0, 1), (0, 2, 1, 1), (0, 0, 1, 1). Podobno będzie to 3, ale nie bardzo widzę jeszcze dlaczego.

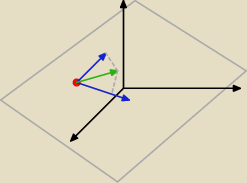
Trivial: Oto chodzi właśnie w podprzestrzeniach liniowych. Mamy świat 3D, w którym znajduje się mały świat 2D. Żadne dozwolone operacje na świecie 2D (dodawanie wektorów, mnożenie przez skalar) nie pozwalają na jego opuszczenie. Mrówki mogą poruszać się w 4 kierunkach (w rozumieniu codziennym, czyli prawo, lewo, do przodu, do tyłu). Ich ruch można opisać poprzez sumę dwóch wektorów bazowych (które nie leżą na jednej linii, wtedy nie wystarczą). Każdy inny wektor tej płaszczyzny można zapisać jako kombinację wektorów bazowych.

Trivial: (1, 0, 1, 0), (−1, 2, 0, 1), (0, 2, 1, 1), (0, 0, 1, 1). Można zauważyć, że (0, 2, 1, 1) = 1*(1, 0, 1, 0) + 1*(−1, 2, 0, 1), a zatem trzeci wektor nie wnosi nic nowego jeśli chodzi o przestrzeń.

dawid: ale jak ty to tak szybko zauważyłeś ?

Trivial: Współczynniki nie były jakieś specjalnie trudne do odgadnięcia. Miejsca charakterystyczne na które trzeba zwracać uwagę to zera. W ogólnym przypadku trzeba rozwiązać układ równań Ax = 0 gdzie A jest macierzą utworzoną z wektorów, a x = (x₁,x₂,...,x_n) poszukiwaną kombinacją liniową. W przypadku, gdzie wektory są liniowo niezależne jedynym rozwiązaniem jest x = (0,...,0).

dawid: czyli w takich przypadkach, aby sprawdzić czy jaki jest wymiar trzeba posprawdzać odpowiednie wektory ? tylko skąd u Ciebie tam się wzięły te dwie jedynki?

Trivial: Te jedynki napisałem żeby dobrze było widać jakie są stałe kombinacji liniowej (mogłem równie dobrze ich w ogóle nie pisać). Ogólna metoda sprawdzania wymiaru przestrzeni to utworzenie macierzy A z wektorów, dokonanie na niej eliminacji Gaussa (RREF) i policzenie ilości schodków. Mam do tego program, zaraz odpalę.

dawid: eliminacji Gaussa jeszcze nie miałem, hmm ale ten przykład co pokazałeś to on nie jest potwierdzeniem, że da się utworzyć wymiaru 2 ? Bo pokazałeś, że dwa się trzeci z dwóch utworzyć

Trivial: 1 −1 0 0 0 2 2 0 1 0 1 1 0 1 1 1 w3 := w3 − (1)*w1 1 −1 0 0 0 2 2 0 0 1 1 1 0 1 1 1 w2 := w2/(2) 1 −1 0 0 0 1 1 0 0 1 1 1 0 1 1 1 w1 := w1 − (−1)*w2 w3 := w3 − (1)*w2 w4 := w4 − (1)*w2 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 1 Kolumna 3 oznaczona jako wolna w4 := w4 − (1)*w3 1 0 1 0 ← schodek 0 1 1 0 ← schodek 0 0 0 1 ← schodek 0 0 0 0 wymiar: 3

Trivial: Widać, że 3 wektor nie wnosił nic nowego, bo 'schodek' był w kolumnach: 1, 2, 4. W kolumnie 3 schodka nie było.

Trivial: Żeby mieć potwierdzenie, trzeba sprawdzić czy pozostałe 3 wektory są liniowo niezależne. Metoda Gaussa szybko to sprawdza.

dawid: no ale jak ktoś nie zna eliminacji gaussa i nie wie co to schodek [jak ja], to jak znaleźć coś takiego. Bo wątpię abym mógł to wykorzystać przy rozwiązaniu, a jakoś sprawdzić muszę. A to twoje: (0, 2, 1, 1) = 1*(1, 0, 1, 0) + 1*(−1, 2, 0, 1) i trzeci wektor nie wnosi nic nowego, a gdzie wykorzystujemy 4? bo póki co widzę, że wykorzystujemy dwa wektory to opisania trzeciego.

dawid: czyli (0, 0, 0, 0) = a*(1, 0, 1, 0) + b * (−1, 2, 0, 1) + c * (0, 0, 1, 1) o to chodzi? jeżeli to sprawdzimy to mamy z głowy ?

Trivial: Tak. Jeśli jedynym rozwiązaniem jest a=b=c=0 to są liniowo niezależne.

dawid: i z tego co wyżej napisałem, otrzymujemy, że a = b = c = 0, więc jest liniowo niezależny

dawid: ok, a czy można zastosować metodę taką brute force, czyli wpierw spróbować: (0, 0, 0, 0) = a*(1, 0, 1, 0) + b * (−1, 2, 0, 1) + c * (0, 0, 1, 1) + d * (0, 2, 1, 1) i jeżeli tutaj będzie liniowo zależny to znaczy, że wymiar jest mniejszy niż 4?

Trivial: Zauważ, że same zera zawsze są rozwiązaniem. Czasem istnieją rozwiązania niezerowe. Interesują Cię tylko one. Żeby to szybko rozwiązać musisz tak poredukować wektory ze sobą, żeby każdy z nich wprowadzał coś nowego, tj. np. (1,2,3,4) (0,2,3,1) (0,0,2,3) (0,0,0,4) Tutaj widać, że są liniowo niezależne. Mamy 4 "schodki", a idąc od dołu, każdy wektor wprowadza coś nowego. Dozwolone operacje które nie wpływają na niezależność liniową to dodawanie oraz mnożenie przez niezerowy skalar.

dawid: ale moglibyśmy np.: sprawdzać wszystkie metody, tj.: czy da się stworzyć jakiś jeden wybrany z reszty wektorów a = b + c + d b = a + c + d c = a + b + d d = a + b + c wiem, że jest to czasochłonne, ale chyba można tak zrobić? jak nie zna się eliminacji gaussa ?

dawid: dim(A + B)=dim(A) + dim(B) − dim(A∩B) Twoim zdaniem da się to jakoś łatwo udowodnić ?

Trivial: Takie sprawdzenie jak napisałeś wyżej nie wystarcza. Można policzyć także wyznacznik, ale Gauss jest szybszy. Jeśli chodzi o te wymiary... Nieformalnie można tak: Niech n = dim(A); k = dim(B). A+B to przestrzeń { α*a + β*b | a∊A, b∊B }. Intuicyjnie można stwierdzić, że skoro mamy wszystkie kombinacje liniowe z przestrzeni A,B to przestrzeń A+B ma wymiar max{n,k}. Z kolei A∩B to przestrzeń, która zawiera tylko wektory występujące w obu przestrzeniach na raz (na przecięciu). Zatem dim(A∩B) = min{n,k}. Podstawiamy do wzoru i mamy: dim(A+B) = dim(A) + dim(B) − dim(A∩B) max{n,k} = n + k − min{n,k} max{n,k} + min{n,k} = n + k ← tu już OK, gdyż max{a,b} + min{a,b} = a+b.

dawid: dobra będę leciał spać , mógłbyś podrzucić jakiś pomysł postaram się coś z rana pomyśleć, bo kurczę ciekawe są te zagadnienia bardzo dziękuję za dzisiejszą pomoc

dawid: to będę musiał się zastanowić jak to formalnie zapisać, na pewno trzeba będzie udowodnić min i max, ale da się chyba prościej

dawid: myślałem, żeby wykorzystać twierdzenie Steinitza, ale to rano pomyślę dogłębniej tym czasem dobranoc i jeszcze raz wielkie dzięki

Trivial: dobranoc.

Trivial: Chociaż jak teraz tak myślę, to te maksy to totalny bezsens, które w dodatku nie działa. Nie chce mi się już dzisiaj tego rozwiązywać, więc zdam się na gotowe rozwiązanie. http://www.proofwiki.org/wiki/Dimension_of_Sum_and_Intersection_of_Vector_Spaces

dawid: ok, zrobiłem to sam nawet udowodniłem dwa lematy i wykorzystałem przy udowodnieniu a z innej beczki: Czy przestrzeń jest liniowa: L(x, y) = (2x − y, x + 3y − 1, 5x + 2y) wiem, że tutaj mamy R² → R³ i trzeba to robić z definicji: u₁ = x₁ + y₁ u₂ = x₂ + y₂ u = (x, y) f(u₁ + u₂) = f(u₁) + f(u₂) f(x₁ + x₂, y₁ + y₂) = (2(x₁ + x₂) − (y₁ + y₂), (x₁ + x₂) + 3(y₁ + y₂) − 1, 5(x₁ + x₂) + 2(y₁ + y₂) = (2x₁ + 2x₂ − y₁ − y₂, x₁ + x₂ + 3y₁ + 3y₂ − 1, 5x₁ + 5x₂ + 2y₁ + 2y₂) I teraz chyba nie da się tego odpowiednio pogrupować, aby zachodziła suma tylko jak to uzasadnić? W poleceniu jest napisane również, aby dla przestrzeni liniowych znaleźć ich jądro, wymiar i oblicz rząd przekształcenia, opisz obraz. Dobrze myślę?

Trivial: Wystarczy dać jeden kontrprzykład. Miejscem, w którym należy zacząć jest −1 w drugiej współrzędnej L(x,y). Prosty test: L(0,0) = (0,−1,0) powinno być zerem, a nie jest → przestrzeń nie jest liniowa. Jądro przekształcenia liniowego to te wektory, które przekształcenie sprowadza do zera. Przykład: Dla przekształcenia liniowego L(x,y,z) = (y−x, z−y, x−z) jądrem są wektory postaci: c*(1,1,1), gdyż: L(c*(1,1,1)) = c*L(1,1,1) = c*(0,0,0) = (0,0,0). Żeby znaleźć wszystkie takie wektory, trzeba rozwiązać układ równań Au = 0. Dla tego przykładu mamy A: −1 1 0 0 −1 1 1 0 −1

maciek: ale rozpisanie jest dobre?

dawid: i z góry przepraszam za zmianę nicku, ale pomagałem innym

dawid: mam jeszcze dwa przykłady, jeden z nich: L(x, y, z) = (3x + 5y − 2z, 2x − y) Widzę, że R³ → R² u₁ = x₁ + y₁ + z₁ u₂ = x₂ + y₂ + z₂ u₃ = x₃ + y₃ + z₃ f(u₁ + u₂ + u₃) = f(u₁) + f(u₂) + f(u₃) f(x₁ + ... + z₃) = (3(x₁ + x₂ + x₃) + 5(y₁ + y₂ + y₃) − 2(z₁ + z₂ + z₃), 2(x₁ + x₂ + x₃) − (y₁ + y₂ + y₃) = (3x₁ + 3x₂ + 3x₃ + 5y₁ + 5y₂ + 5y₃ − 2z₁ − 2z₂ − 2z₃, 2x₁ + 2x₂ + 2x₃ − y₁ − y₂ − y₃ ) i jak to dalej doprowadzić do normalnej formy ?

Trivial: Ja nie wiem co robisz przy rozpisywaniu. To się robi tak: u = (u₁,u₂,u₃) v = (v₁,v₂,v₃) u+v = (u₁+v₁, u₂+v₂, u₃+v₃) L(u+v) = (..., ...) L(u)+L(v) = (.., ..) + (.., ..) = (..., ...) Równe?

Trivial: A tak na marginesie, każde skończenie wymiarowe przekształcenie liniowe można zapisać w postaci mnożenia przez macierz. Jeżeli możesz tak zapisać, to od razu masz dowiedzione, gdyż macierze spełniają wszystkie warunki przekształcenia liniowego. L(x,y,z) = (3x + 5y − 2z, 2x − y) W formie macierzowej: [ x ]

	3x + 5y − 2z 2x − y
AL [ y ] =

[ z ] Odczytujemy wartości macierzy A_L, żeby się zgadzało: 3 5 −2 2 −1 0 I to wystarczy, żeby przekształcenie było liniowe.

dawid: Nie miałem jeszcze macierzy. A jak to odczytaliśmy to co dalej ? A czy mógłbyś rozpisać tą swoją metodą skróconą ten przykład? Bo wzorowałem się na : http://www.matematyka.pl/252971.htm

Trivial: Gdy już odczytamy to tyle. Nie zawsze da się to zrobić, ale jeśli się da to od razu wiemy, że przekształcenie jest liniowe. a) f(x) = 2x b) f(x) = ln(x²+2) c) f(x₁,x₂,x₃) = (x₁², x₂², x₃²) d) f(x) = (5x, x) e) f(x₁,x₂,x₃) = (x₁,x₂+1) a) Zapisujemy jako [2]*[x] (macierzą jest sama dwójka), czyli przekształcenie jest liniowe. OK b) Nie da się zapisać w postaci macierzowej. Dajemy kontrprzykład i załatwione. Np. f(0) powinno być 0, a nie jest, gdyż f(0) = ln(2) FAIL Dlaczego zawsze f(0) musi być zerem? f(0) = f(0+0) =^{f liniowe}= f(0) + f(0) = 2*f(0) f(0) = 2*f(0) → f(0) = 0 dla dowolnego przekształcenia liniowego. c) Tutaj również nie da się zapisać w postaci macierzowej. Potrzebny jest kontrprzykład. Można policzyć np. f(2) = (4,4,4), ale f(2) = f(1+1) = f(1)+f(1) = 2*f(1) = 2*(1,1,1) = (2,2,2). FAIL d) Zapisujemy jako [5 1][x] (macierzą jest [5 1]). OK d) Nie da się zapisać − kontrprzykład: f(0,0,0) = (0,1) ≠ (0,0) FAIL

Trivial: W c) miałem na myśli f(2,2,2) = (4,4,4) oraz f(2,2,2) = f((1,1,1) + (1,1,1)) = f(1,1,1) + f(1,1,1) = 2*f(1,1,1) = (2,2,2)

dawid: bardziej chodziło mi o takie rozpisanie: u = (u1,u2,u3) v = (v1,v2,v3) u+v = (u1+v1, u2+v2, u3+v3) tego przykładu z 00:16

dawid: ?

Trivial: L(x,y,z) = (3x + 5y − 2z, 2x − y) + L(u,v,w) = (3u + 5v − 2w, 2u − v) L(x+u, y+v, z+w) = (3(x+u) + 5(y+v) − 2(z+w), 2(x+u) − (y+v)) OK

Trivial: Mnożenie przez skalar jest jeszcze prostsze do pokazania.

dawid: o rany a ja tyle rozpisywałem a jak wyznaczyć z tego jądro i obraz ?

Trivial: Trzeba rozwiązać równanie L(x,y,z) = 0 (znaleźć wszystkie rozwiązania, a nie tylko jedno)

dawid: Ale równanie odnośnie obrazu czy jądra? (3x + 5y −2z), (2x − y) = (0,0,0)

⎧	3x + 5y − 2z = 0
⎩	2x − y = 0

⎧	3x + 10x − 2z = 0
⎩	y = 2x

⎧	z = 13/2x
⎩	y = 2x

I co dalej ?

dawid:

Krzysiek: rozwiązując to równanie szukasz jądro odwzorowania i ta równość jest dziwnie napisana (3x+5y−2z,2x−y)=(0,0) a co dalej? np. x=a, a∊R−parametr i rozwiązanie to wektor postaci (a,2a,13/2)=a(1,2,13/2) KerL=Lin{(1,2,13/2)}

dawid: a obraz jak zapisać ?

Krzysiek: L(x,y,z)=(3x+5y−2z,2x−y) ImL={(3x,2x)+(5y,−y)+(−2z,0),x,y,z∊R}={x(3,2)+y(5,−1)+z(−2,0),x,y,z∊R}=LinL{ (3,2),(5,−1),(−2,0)}

dawid: a mógłbyś napisać na jakiej podstawie ? Skąd takie wnioskowanie

Krzysiek: ImL=def={L(u);u∊R³} (w tym przypadku R³, bo L:R³→R² )

dawid: ok, mógłbym mieć jeszcze pytanie jak: a) obliczyć rząd przekształcenia [ korzystając z tw. o wymiarze przekszt. liniowej b) znaleźć wymiar jądra ? Mam przykład, który będę chciał zrobić sam w całości, ale wpierw chcę dowiedzieć się jak zrobić te powyższe punkty

Krzysiek: b) chyba widać,że wymiar jądra w tym zadaniu to 1. a) skorzystaj z tego,że; rzL+dimKerL=dimU (L:U→V)

dawid: b) dopiero uczę się podstawowych rzeczy i jeszcze tego nie widzę, mógłbyś to bardziej opisać ?

Krzysiek: liniowa powłoka składa się z jednego wektora no więc wymiar to 1. sprawdź Sam ile wynosi dimImL czyli zbadaj liniową niezależność wektorów (3,2),(5,−1),(−2,0) i maksymalna ilość wektorów niezależnych to wymiar przestrzeni.

dawid: a(3, 2) + b(5, −1) + c(−2, 0) = (0, 0) (3a, 2a) + (5b, −b) + (−2c, 0) = (0, 0) 3a + 5b − 2c = 0 2a − b = 0 13a = 2c b = 2a c = (13/2)a b = 2a teoretycznie tak się bada liniową niezależność, chociaż już wszystko mi się miesza

angelika: SSSuper stronkaaaaaaa

dawid: a odnośnie a) o to chodzi: Rząd macierzy przekształcenia liniowego jest równy wymiarowi bazy w R( f ), co zapisujemy: Rząd Af =dim R( f )

Krzysiek: a) masz policzyć rzL skoro wiesz,że dimKefL=1, dimU=dimR³=3 to rzL=3−1=2 zatem rząd tego odwzorowania to 2.

dawid: Ok, to teraz mam przykład ostatni, który postaram się sam zrobić: R³ → R³ L(x,y,z) = (x + y + z, −2x − z, −2y − z) L(u, v, w) = (u + v + w, −2u − w, −2v − w) _______________________________ L(x + u, y + v, z + w) = ( (x + u), + (v + y) + (z + w), −2(x + u), −(z + w), −2(v + y) − (z + w)) Więc ok, zatem przekształcenie jest liniowe.

dawid: ?

dawid: Teraz L(x, y, z) = (0,0,0) (x + y + z, −2x − z, −2y , −z) = (0,0,0) x + y + z = 0 −2x − z = 0 −2y − z = 0 x + y + z = 0 z = −2x = −2y x + y −2x = 0 −x + y = 0 y = x Zatem: z = −2x y = x x = a, a ∊ R (a, a, −2) = a(1, 1, −2) KerL=Lin{(1,1,−2)} dobrze czy źle ? I jakbym mógł poprosić − dlaczego tak wektor zapisujemy ?

dawid:

dawid:

Krzysiek: dobrze wyznaczone jądro odwzorowania. zapisuj wektor jak chcesz... ważne żebyś tak samo zapisywał jak na Twoich ćwiczeniach/wykładach

dawid: to teraz obraz: L(x, y, z) = (x + y + z, −2x − z, −2y − z) ImL = {(x, −2x, 0), (y, 0, −2y), (z, −z, −z), x, y, z ∊ R } = = {x(1, −2, 0), y(1, 0, −2), z(1, −1, −1), x , y, z ∊ R } = = LinL{(1, −2, 0), (1, 0, −2), (1, −1, −1)} ok ?

Krzysiek: ok. jak będziesz wyznaczał wymiar obrazu to zbadaj czy te 3 wektory są liniowo niezależne.

dawid: Czyli: a(1, −2, 0) + b(1, 0, −2) + c(1, −1, −1) = (0,0,0) zgadza się ? i teraz rozwiązać układ:

⎧	a + b + c = 0
⎨	−2a − c = 0
⎩	−2b − c = 0

?

Krzysiek: zamiast badać z definicji szybciej jest policzyć wyznacznik złożony z tych wektorów, jeżeli jest różny od zera to są liniowo niezależne.

dawid: jeszcze tego nie miałem − wyznaczników

⎧	a + b + c = 0
⎨	c = −2a
⎩	c = −2b

c = −2a = −2b a + b − 2a = 0 −a + b = 0 b = a c = −2a nie są liniowo niezależne ?

Krzysiek: nie są.

dawid: ale dalej nie umiem wyznaczyć z tego wymiar jądra − jak nie są liniowo niezależne

dawid: ?

Krzysiek: chyba wymiar obrazu nie umiesz wyznaczyć,bo wymiar jądra odwzrorowania to 1. wektor (1,−1,−1) jest liniowo zależny z pozostałymi.

dawid: wymiaru obrazu nie umiem wyznaczyć? w jakim sensie. i jak obliczyłeś wymiar jądra − skąd to widać, tj.: jak jest liniowo zależny to zawsze jest 1 ?

Krzysiek: przecież jądro odwzorowania składa się tylko z jednego wektora więc wymiar to 1. obraz odwzorowania składa się z 3 wektorów ale są one liniowo zależne więc wymiar obrazu nie jest równy 3. tylko 2. bo wektory (1,−2,0) , (1,0,−2) są liniowo niezależne.

dawid: a rząd przekształcenia to będzie: 3 − 1 = 2 ?

dawid:

Krzysiek: tak

dawid: Czyli tak jakby to wszystko , a przed zakończeniem mógłbym prosić o jedną rzecz, mianowicie, czuje jeszcze się nie pewnie w tym: "przecież jądro odwzorowania składa się tylko z jednego wektora więc wymiar to 1" nie widzę tego

dawid: ?

dawid: I jaki kontrprzykład może być dla pierwszego przykładu, czyli: L(x, y) = (2x − y, x + 3y − 1,5x + 2y)

dawid: ?

dawid:

Krzysiek: KerL=Lin{(1,1,−2)} aby policzyć wymiar jądra odwzorowania sprawdzasz ile jest wektorów liniowo niezależnych w powłoce liniowej (Lin) tutaj jest tylko 1 wektor więc nie ma co sprawdzać. więc dimKerL=1 a nie wiem o co Tobie chodzi z tym kontrprzykładem

dawid: chodzi mi o to, że jeżeli nie jest przestrzenią liniową, to nie powinniśmy podać kontrprzykładu ? ten przykład : L(x, y) = (2x − y, x + 3y − 1, 5x + 2y)

Krzysiek: jeżeli uważasz,że nie jest odwzorowaniem liniowym to musisz to jakoś wykazać, możesz podać kontrprzykład albo badać z definicji

dawid: (x, y) = (2x − y, x + 3y − 1, 5x + 2y) (u, v) = (2u − v, u + 3v − 1, 5u +2v) (x + u, y + v) = (2(x + u) − (y + v), (x + u) + 3(y + v) − 2, 5(x + u) + 2(y + v)) a jest? mi ta jedynka tutaj nie pasuje

Krzysiek: nie jest ale Ty to coś dziwnie zapisujesz... L(x+u,y+v)=(2(x + u) − (y + v), (x + u) + 3(y + v) − 1, 5(x + u) + 2(y + v))≠L(x,y)+L(u,v)

dawid: i taki zapis jest poprawny, tj.: udowadnia nam, że coś nie jest / jest przestrzenią liniową ?

Krzysiek: no jeszcze trzeba rozpisać L(x,y), L(u,v) by było widać,że to jest różne.(masz już rozpisane tylko nie pisz (x,y)=... tylko L(x,y)=... )

dawid: ok, a mógłbyś podać jeszcze jakiś kontrprzykład ?

Krzysiek: a po co kontrprzykład? skoro już ten warunek nie zachodzi... poza tym Trivial podał kontrprzykład (jeżeli dobrze widzę,że to ten sam przykład)

dawid: mam jeszcze ostatnie pytanie, jak wyznaczyć dim(Im(L)) − w przykładzie drugim czyli: L(x,y,z) = (3x + 5y − 2z, 2x −y) ?

Krzysiek: patrz co napisałem 28 kwi 2013 15:34