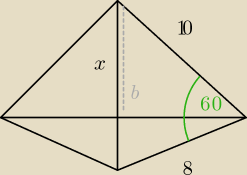
 W trójkącie ABC |AB| = 8, |BC| = 10, zaś |kąt ABC| = 60 stopni. Oblicz objętość i pole
powierzchni bryły powstałej z obrotu trójkąta ABC dookoła prostej zawierającej bok AC.
jak zwykle licze licze i nie moge sie doliczyc
PABC= 1/2 * 10 *8 * sin60 = 20√3
x2=100+64 − 80
x=√84
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
20√3= h *1/2 * √84
W trójkącie ABC |AB| = 8, |BC| = 10, zaś |kąt ABC| = 60 stopni. Oblicz objętość i pole
powierzchni bryły powstałej z obrotu trójkąta ABC dookoła prostej zawierającej bok AC.
jak zwykle licze licze i nie moge sie doliczyc
PABC= 1/2 * 10 *8 * sin60 = 20√3
x2=100+64 − 80
x=√84
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
20√3= h *1/2 * √84
| 40√3 | ||
h= | ||
| √84 |
| 400 √300 | ||
czyli V z tego ... KOSMICZNIE RACZEJ  | π | |
| 21 √7 |
| 400 √48 | ||
I ANALOGICZNIE DRUGI v −− | π | |
| 4√7 |
 gdzie się machnęłam
gdzie się machnęłam 
| 40√3 | 20√3 | |||
h= | = | |||
| 2√21 | √21 |
| 1 | 1 | 1 | ||||
V= | πR2*h1+ | πR2*h2= | πR2*(h1+h2)= [h1+h2=AC=2√21] | |||
| 3 | 3 | 3 |
| 1 | 20√3 | |||
= | π*( | )2*2√21= | ||
| 3 | √21) |
| 1 | 400*3 | |||
= | π* | *2√21= | ||
| 3 | 21 |
| 800π√21 | ||
= | ||
| 21 |
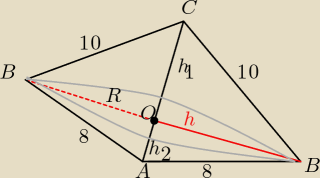 Pc=πR*10+πR*8=πR*18
podstaw za R
Pc=πR*10+πR*8=πR*18
podstaw za R
 zaraz to przeanalizuje
zaraz to przeanalizuje
