pola trójkątów pokres: W trójkącie ABC punkty DE określają bok AB na 3 odcinki równej długości. Punkt H jest środkiem boku AC. Punkty GF określają bok BC na 3 odcinki równej długości. Wynika, że pole trójkąta EGH 5/18=Ptr.ABC

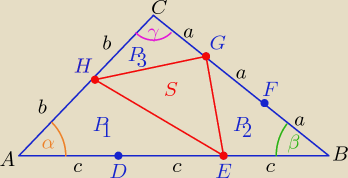
Eta: |AB|=3c, |BC|=3a , |AC|=2b , R−− dł. promienia okręgu opisanego na trójkącie ABC P(EGH)= S

	3a*2b*3c		18abc
P(ABC)=		=
	4R		4R

	3a		3a
Z twierdzenia sinusów:		=2R ⇒ sinα=
	sinα		2R

	3c		3c
		=2R ⇒ sinγ=
	sinγ		2R

	2b		2b
		=2R ⇒ sinβ=
	sinβ		2R

	3abc		2abc		ab		3abc
P1= bc*sinα=		, P2=ac*sinβ=		, P3=		*sinγ=
	2R		2R		2		4R

	18abc		6abc		4abc		3abc
S=P−(P1+P2+P3)=		−(		+		+		)=
	4R		4R		4R		4R

	5abc
=
	4R

	5abc
S=
	4R

	S		5		5
to		=		⇒ S=		P
	P		18		18

c.n.u