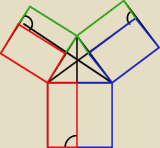
Zastosowanie pojecia pola w dowodzeniu twierdzeń Anonim: Witam! Mam problem z zadaniami. Chodzi o zadania z zastosowaniem pojęcia pola w dowodzeniu twierdzeń (wykorzystanie pola trójkąta i funkcji trygonometrycznych) 1) Na bokach trójkąta ostrokątnego zbudowano kwadraty, następnie poprowadzono proste zawierające wysokości tego trójkąta. Proste podzieliły kwadraty na 6 prostokątów. Wykaż, że prostokąty zaznaczone tym samym kolorem mają równe pola. (Rysunek) 2) W trójkąt prostokątny o przyprostokątnych mających długość a i b (a>b) wpisano prostokąt w taki sposób, że dwa kolejne boki prostokąta zawierają się w ramionach kąta prostego, a jeden jego wierzchołek leży na przeciwprostokątnej. Stosunek boków prostokąta jest równy 1:2. Oblicz długość krótszego boku prostokąta. Rozważ 2 przypadki. 3)Punkt M należy do podstawy AB trójkąta równoramiennego ABC, M≠A i M≠B. Wykaż, że suma odległości punktu M od ramion trójkąta jest równa wysokości trójkąta, poprowadzonej z punktu A. 4)Wykaż, że jeśli suma wysokości trójkąta jest 9 razy większa od długości promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.

	ab 2a+b		ab a+2b
ODPOWIEDZI do zadania 2 :		lub

WSKAZÓWKA do zadania 3 : przedstaw pole trójkąta ABC jako sumę pól trójkątów AMC i MBC WSKAZÓWKA do zadania 4 : ulaleznij wysokości o promień okręgu wpisanego w trójkąt od pola i długości boków trójkąta. Zauważ, że dla dowolnych liczb dodatnich x,y prawdziwa jest

	x y		y x
nierówność		+		≥2, przy czym równość ma miejsce wtedy, gdy x=y

(odpowiedzi i wskazówek nie można wykorzystać rzecz jasna w założeniach) Będę wdzięczna za jakąkolwiek pomoc. Z góry dziękuje

Piotruś: Umiałby ktoś zrobić 1) i 3)?

Piotruś: Pomocy