W trójkącie ABC bok AC jest 3 razy dłuższy od boku BC. Na boku AB zaznaczono pun
kirakira: Bardzo proszę o pomoc w zadaniu.
W trójkącie ABC bok AC jest 3 razy dłuższy od boku BC. Na boku AB zaznaczono punkt D. Oblicz
stosunek pola koła opisanego na trójkącie ADC do pola koła opisanego na trójkącie DBC
24 kwi 21:51
Bogdan:
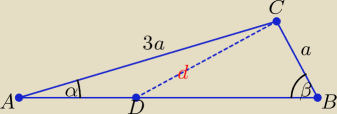
| | 3a | | a | |
Na podstawie twierdzenia sinusów: |
| = |
| ⇒ sinβ = 3sinα |
| | sinβ | | sinα | |
R − długość promienia okręgu opisanego na ADC,
r − długość promienia okręgu opisanego na DBC.
| | d | | d | |
Z wzoru sinusów dla trójkątów ADC i DBC: |
| = 2R, |
| = 2r |
| | sinα | | 3sinα | |
| 2R | | | | R | | πR2 | |
| = |
| ⇒ |
| = 3 ⇒ |
| = ... |
| 2r | | | | r | | πr2 | |
24 kwi 22:53
