calki ewel: witam, czy moglby ktos mi pomoc rozwiazac zadanko? Obliczyc pole P P: y=e^x, y=lnx, x+y=1, x=2

AS: Obliczenie pomocnicze I = ∫lnxdx Obliczenia przez części (per partes) Podstawienia: u = lnx dv = dx

	dx
du =		v = x
	x

	dx
I = u*v − ∫v*du = x*lnx − ∫x*		= x*lnx − ∫dx = xlnx − x
	x

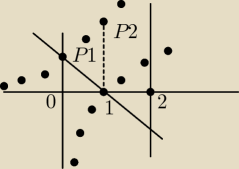
Pole pierwszego obszaru 1 1 1 P1 = ∫(e^x − (1 − x))dx = ∫(e^x + x − 1) = e^x + x²/2 − x | 0 0 0 (e¹ + 1²/2 − 1) − (e⁰ + 0²/2 − 0) = e + 1/2 − 1 − 1 = e − 1 1/2 2 2 2 2 2 P2 = ∫(e^x − lnx)dx = ∫e^xdx − ∫lnxdx = e^x | − (xlnx − x) | = 1 1 1 1 1 = e² − e¹ − (2ln2 − 2 − 1ln1 + 1) = e² − e − ln4 +2 + 0 − 1 = e² − e + 1 − ln4 Pole łączne P = P1 + P2 = e − 1 1/2 + e² − e + 1 − ln4 P = e² − ln4 − 1/2 ≈ 5.5003