dowodzenie twierdzeń polo: Punkt M należy do podstawy AB trójkąta równoramiennego ABC, M≠A i M≠B. Wykaż, że suma odległości punktu M od ramion trójkąta jest równa wysokości trójkąta, poprowadzonej z punktu A.

help: pomoże ktoś?

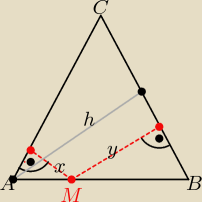
Bogdan: |AC| = |BC| = a Pole trójkąta

	1		1
P =		*|BC|*h =		ah
	2		2

oraz

	1		1		1		1		1
P =		*|AC|*x +		*|AC|*y =		ax +		ay =		a(x + y)
	2		2		2		2		2

Dalej sam kontynuuj

Bogdan:

	1		1		1		1
poprawka (literówka): P =		*|AC|*x +		|BC|*y =		ax +		ay = ...
	2		2		2		2

help: Do tego momentu sam doszedłem, co dalej?