geometria Lenka6: PROSZĘ O POMOC Oblicz długość promienia okręgu wpisanego w trojkąt rownoramienny, którego boki mają dlugość 5, 5, 6 cm

Bogdan: Pole trójkąta P_Δ = p*r

	1
p =		(a + b + c)
	2

r − długość promienia okręgu wpisanego w trójkąt, a, b, c − długości boków

Lenka6: pomoże ktooś

Lenka6: dzięki

Lenka6: wynik ma być 1.5cm

Lenka6: coś źle obliczasz chyba, bo w odpowiedziach m być 1,5cm

Bogdan: Ile wynosi pole trójkąta, czyli P_Δ ? Ile wynosi połowa obwodu trójkąta, czyli p ?

Lenka6: pole wynosi 9√3 a polowa obwodu 8

Bogdan: Podaj, jak obliczyłaś pole, znajdziemy błąd.

Lenka6: noo wzór a²√3 podzielone przez 4

Bogdan: To jest wzór na pole powierzchni trójkąta równobocznego, a w tym zadaniu nie ma takiego trójkąta.

Bogdan: 503

Lenka6: noo to jaki jest ten wzor?

Bogdan: Zobacz tu 503

Lenka6: no to w takim ukladzie będzie pole rownało się 9

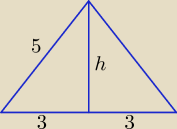
Bogdan: względnie oblicz długość h z twierdzenia Pitagorasa

Bogdan: Jak obliczyłaś 9 ?

Lenka6: no dobra wynik pola jest 9, już to obliczyłam

Bogdan: Można też zastosować wzór Herona.

Bogdan: Nie 9.

Lenka6: możesz mi to obliczyć szybko? bo się gubie

Bogdan: Nie, policz sama. To proste rachunki. Oblicz najpierw długość h z twierdzenia Pitagorasa.

Lenka6: 4

Bogdan: Dobrze. To teraz oblicz pole trójkąta.

Lenka6: 12

Bogdan:

	12
r =		= ...
	8

Bogdan:

	PΔ
r =
	p