zadania z dowodzeniem, planimetria beniamin: Jako że kompletnie nie umiem zadań z dowodzeniem, proszę Was o pomoc w 2 zadaniach. 1. Udowodnij, że odcinek łączący środki dwóch boków dowolnego trójkąta odcina trójkąt podobny do danego. Określ skalę podobieństwa 2. Wykaż, że suma długości średni okręgu opisanego i okręgu wpisanego w trójkąt prostokątny jest równa sumie długości jego przyprostokątnych Z góry dziękuję za pomoc

PW: Zadanie 1. to prościutkie zastosowanie twierdzenia odwrotnego do twierdzenia Talesa − sprawdź treść tego twierdzenia. Można też pokazać, że trójkąty są jednokładne i powołać się na własności jednokładności.

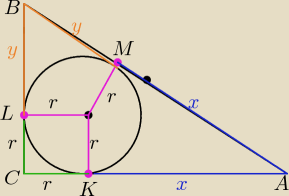
Mila: AC=b BC=a AB=c c=2R − środek okręgu opisanego na Δ prostokątnym leży w środku przeciwprostokątnej CK=CL− punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta KA=MA BM=BL AB=2R=x+y a+b=r+y+r+x=2r+(x+y)=2r+2R 2r+2R=a+b cnw