| 1 | 1−sinx | |||
wyznacz wszystkie rozwiazania rownania | −cosx= | nalezace do przedzialu | ||
| tgx | 2sinx |
| π | ||
x≠kπ i x≠ | +kπ | |
| 2 |
| cosx | 1−sinx | ||
−cosx= | |||
| sinx | 2sinx |
| cosx−sinx*cosx | 1−sinx | ||
− | =0 | ||
| sinx | 2sinx |
| 2cosx*(1−sinx) | 1−sinx | ||
− | =0 wyłączam poza nawias (1−sinx) | ||
| 2sinx | 2sinx |
| (1−sinx)(2cosx−1) | |
=0⇔ | |
| 2sinx |
| 1 | ||
sinx=1 lub cosx= | dokończ | |
| 2 |
| π | ||
a dlaczego wyrzucasz x= | + kπ skoro sinx=0 to x=kπ? | |
| 2 |
| π | ||
a dobra tg=0 to | +kπ tylko tam odwrotnie zapisalas  sorki | |
| 2 |
| π | ||
sinx=1 ⇒x= | +2kπ | |
| 2 |
| 1 | π | π | ||||
cosx= | ⇒x= | +2kπ i x=− | +2kπ tak? | |||
| 2 | 3 | 3 |
| π | 11 | |||
x= | +2kπ i x= | π +2kπ k∊C tak bo to ma byc w przedziale (0,2π) dobrze to rozumiem | ||
| 3 | 6 |
?
| π | π | 5π | ||||
x= | lub x=2π− | = | ||||
| 3 | 3 | 3 |
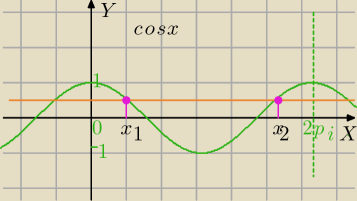y=cos(x)
