 badanie funkcji
Obliczenia są na pewno dobre, chcialem tylko to sobie przy okazji gdzieś zapisać,
a chodzi mi o siatke badania funkcji − zaraz dodam po tym poście.
będę pisać bez obliczeń do prostych granic i pomijał skracanie granic, gdzie wynik już widać na
badanie funkcji
Obliczenia są na pewno dobre, chcialem tylko to sobie przy okazji gdzieś zapisać,
a chodzi mi o siatke badania funkcji − zaraz dodam po tym poście.
będę pisać bez obliczeń do prostych granic i pomijał skracanie granic, gdzie wynik już widać na
| x2+1 | ||
pierwszy rzut oka, np. | = 1 (przy limx→±∞ ) itd. | |
| x2−1 |
| x3 | ||
y= | ||
| x2+12 |
| x3 | |
= 0 | |
| x2+12 |
| 0 | ||
f(0) = | = 0, A(0,0) | |
| 0+12 |
| f(x) | x3 | |||
limx→±∞ | = limx→±∞ | = 1 | ||
| x | x(x2+12) |
| x3 | x3 − x3 − 12x | |||
limx→±∞ f(x) − ax = limx→±∞ | − x = limx→±∞ | = | ||
| x2+12 | x2 + 12 |
| −12x | ||
limx→±∞ | = 0 | |
| x2+12 |
| x3 | 3x2(x2+12) − 2x(x3) | |||
f'(x) = ( | )' = | = | ||
| x2+12 | (x2+12)2 |
| 3x4 + 36x2 − 2x4 | x4 + 36x2 | x2(x2+36) | |||
= | = | ||||
| (x2+12)2 | (x2+12)2 | (x2+12)2 |
| x4 + 36x2 | ||
f''(x) = ( | )' = | |
| (x2+12)2 |
| (4x3 + 2*2*18*x)(x2+12)2 − 2(x2+12)*(2x)*(x4 + 36x2) | |
= | |
| (x2+12)4 |
| 4x(x2+18)(*x2+12)2 − 4x(x2+12)(x4 + 36x2) | |
= | |
| (x2+12)4 |
| (x2+18)(*x2+12) − (x4 + 36x2) | ||
4x * (x2+12) | = | |
| (x2+12)4 |
| (x2+18)(*x2+12) − (x4 + 36x2) | ||
4x * | = | |
| (x2+12)3 |
| x4 + 12x2+18x2 + 216 − x4 − 36x2) | ||
4x * | = | |
| (x2+12)3 |
| 216 − 6x2) | ||
4x * | = | |
| (x2+12)3 |
| 36 − x2) | ||
24x * | = | |
| (x2+12)3 |
| x2 − 36) | ||
− 24x * | = | |
| (x2+12)3 |
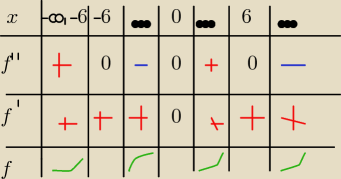 dobrze?
dobrze?

 dzieki
dzieki