Ponawiam prośbę o rozwiązanie: Która z liczb:−1,0,1/2,1 należy do zbioru wartośc danix: Ponawiam prośbę o rozwiązanie: Która z liczb:−1,0,1/2,1 należy do zbioru wartości funkcji f(x)= x2+1/1−x2

Ajtek: Dziedzina x∊R\{−1;1} I teraz podstawiaj:

	x2+1
−1=		wylicz x i zobaczy czy należy do dziedziny. Jak należy, to ta liczba należy
	x2−1

do Z_w.

danix: odp. prawidłowa to 1, ale po wstawieniu za x 1 wychodzi mi równanie sprzeczne 1=x2+1/x2−1 ∥*x2−1 x2−1=x2+1

Ajtek: A jak inne wychodzą

danix: −x2+1=x2+1; f(x)=−1 0=x2+1; f(x)=0 1/2x2−1/2=x2+1; f(x)=1/2 W kluczu jest odp. f(x)=1

Ajtek: Chwila .

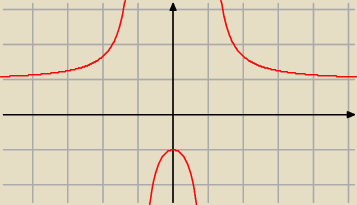
Ajtek: Powinno wyjść −1. Masz rysunek.

danix: może coś nie tak robię w równaniach bo podr. jest rzetelny, więc pomyłki nie ma...

danix: ale przecież tam w mianowniku jest nie x2−1 tylko 1−x2, Może to dlatego?

Ajtek: Ja rozwiązania Tobie gotowego nie podam. Pokazałem co zrobić i tak rób z każdą liczbą. Nie zasłaniaj sie rzetelnościa podręcznika.

Ajtek: Sorry, źle zerknąłem, zmienia to postać rzeczy.

	x2+1
Czyli sprawdzasz, np. 0=		.
	1−x2

danix: dzięki − będę próbował

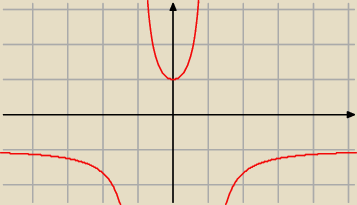
Ajtek: Mój błąd, oczywiście, przepraszam za zamieszanie. Teraz wyjdzie 1 .

danix: spoko − też tego nie widziałem, ale tak to jest jak się liczy kilka godzin, przychodzi zmęczenie i przy okazji ślepota

Ajtek: Nie tyle ślepota, co rutyna.

danix: ale mam nauczkę by odpuścić zadanie i wrócić do niego później, a ja mam tak, że jak nie rozwiążę czegoś to mnie drażni, że czegoś nie rozwiązałem... dzięki wielkie bo bym siedział dalej i szedł z tym zadanie donikąd

Ajtek: Szedłbyś donikąd przez moje niedopatrzenie . Zwracaj uwagę na takie błędy .

Ajtek: Powodzenia