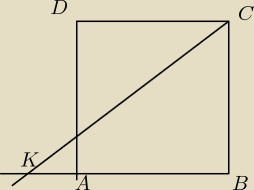
DOWÓD+RYSUNEK!!!!!!!!!! V.Abel: Z wierzchołka C prostokąta ABCD poprowadzono prostą przecinającą bok AB i AD odpowiednio w

	|AB|		|AD|
punktach K i L. Wykaż, że		=
	|AK|		|AL|

Czy rysunek jest ok? P.S nie wiem do końca jeszcze jak tu się rysuje prostokąty, więc proszę przyjmijcie, że to jest prostokąt nie będący kwadratem

V.Abel: *korekta w treści jest "(...) prostą przecinającą prostą AB i AD odpowiednio(...)" /jeśli to coś zmienia/

V.Abel: hej bardzo proszę o pomoc

pigor: ..., a czy na pewno dobrze napisałeś tezę

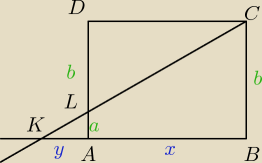
aniabb: z podobieństwa trójkątów (kkk) albo z Talesa wynika że

b		x+y
	=
a		y

	AD		BK
Zatem najbliższe Twojemu jest		=		ale to jednak różnica
	AL		AK

V.Abel: dobra, racja, przepraszam− aniabb napisała poprawną tezę, co jednak nie przeczy temu, że na podstawie Talesa zbytnio nie wychodzi..

Mila: Całą masę proporcji możesz ułożyć: ΔALK∼ΔBCK cecha kkk, boki proporcjonalne ΔAKL jednokładny do ΔDCL, zatem boki są proporcjonalne. Tylko nie wiadomo co trzeba uzasadnić, pisz precyzyjnie treść zadania.