zadanie na dobranoc Saizou : ma ktoś jakieś przyjemne zadanko z planimetrii na dobranoc

Eta: Aaa ... szare, bure ........

Saizou : ale najpierw zadanko (btw. mam rudego kota )

Ajtek: Dobr wieczór Eta, Saizou . Humory widzę dopisują .

Saizou : Witaj Eta i Ajtek i to bardzo trzeba cieszyć się życiem

Dominik: W trapezie ABCD (AB || CD) dwusieczna kąta wewnętrznego ABC jest prostopadła do ramienia AD trapezu i ma z tym ramieniem punkt wspólny P. Punkt P dzieli ramię AD w stosunku 2:1 (dłuższa część leży bliżej dłuższej podstawy). Oblicz stosunek pola trójkąta ABP do pola czworokąta PBCD. przyjemne, latwe zadanko.

Bogdan: Zadania z matury z 1868 r. Zadanie 1. Znaleźć cztery liczby tworzące kolejno proporcję, których suma jest równa 45, różnica dwóch kolejnych zmniejszona o 1 jest równa różnicy dwóch pozostałych, a suma kwadratów ostatniej i pierwszej zmniejszonej o 1 jest równa sumie kwadratów pozostałych liczb zwiększonej o 30. Zadanie 2. W trójkącie wysokość poprowadzona z wierzchołka dzieli kąt w wierzchołku w stosunku 2 do 1, a podstawę odpowiednio na odcinki długości 214 i 50. Wyznaczyć wszystkie boki i kąty w tym trójkącie. Zadanie 3. Kula wpisana w stożek prosty połowi jego wysokość, a płaszczyzna równoległa do podstawy i styczna do kuli odcina koło o promieniu 7. Obliczyć objętość kuli i stożka. Zadanie 4. Znaleźć trójkąt równoramienny, znając kąt w jego wierzchołku i odległość środków koła wpisanego i opisanego na tym trójkącie.

Dominik: 1868?

Saizou : a miało być przyjemnie

Ajtek: Witaj Bogdan . Przyjemne zadanka .

Eta:

Ajtek: Wiem dlaczego puszczasz oko Eta . Tzn. chyba wiem.

Bogdan: Tak, to są zadania z roku 1868 poziomu (jak byśmy dzisiaj powiedzieli) podstawowego. Są jeszcze trzy zadania poziomu wyższego. Poziom wyższy. Zadanie 1. W dany stożek prosty wpisać walec o największej objętości. Obliczyć stosunek jego wysokości do wysokości stożka i stosunek promienia podstawy walca do promienia podstawy stożka. Zadanie 2. W trójkącie sferycznym o bokach a, b, c i kątach A, B, C znany jest kąt C = 75°12' i bok a = 52°25'. Obliczyć pozostałe boki i kąty trójkąta. Zadanie 3. Skonstruować parabolę, znając jej ognisko i jego odległość od stycznej do paraboli w danym punkcie.

Ajtek: Te trzy już są mniej przyjemne . Z pierwszym bym powalczył, ale reszta...

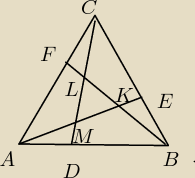
PW: Saizou, Ty jak Pascal, który powiadał, że inni walczą z matematyką wymawiając się bólem zębów, a on walczy z bólem zębów rozwiązując zadania. Czeka Cię wielka przyszłość. To znasz? W trójkącie równobocznym o polu P na bokach obrano punkty D, E i F dzielące te boki w stosunku 1:2, tak jak na rysunku. Wyliczyć, jaką część P zajmuje trójkąt KLM.

Saizou : na razie głowię się nad zadaniem od Dominika. Trzeba się w końcu przełamać i powalczyć z geometrią, która u mnie kuleje

Dominik: wskazowke?

ciekawski: Bogdan, mogłbyś podać link do tej całej matury? Chętnie bym obejrzał całość.

Dominik: http://malzol.w.interia.pl/zadania__maturalne__z__1868__rok.htm

Saizou : nie, trzeba być konsekwentnym, jak się zaczęło to trzeba skończyć

Bogdan: Podaje jako ciekawostkę. W Zbiorach Specjalnych Biblioteki Uniwersytetu Wrocławskiego zachowały się dokumenty z matury w Gimnazjum Świętej Elżbiety w roku 1868. Do matury przystąpiło siedmiu abiturientów, którzy zdawali kolejno: języki (niemiecki − wszyscy, kilku francuski, a jeden − polski). W dalszej kolejności zdawano grekę, łacinę lub hebrajski, matematykę, historię z geografią i fizykę. Trzeciego marca 1868 o godzinie 8:15 rozpoczął się egzamin z matematyki. Ostatni kandydat opuścił salę o 12:30. Komisji egzaminacyjnej przewodniczył dr Kampmann, a prace z matematyki poprawiał Kambly. Zestaw z matematyki obejmował cztery zadania. Zadania na ogól rozwiązywano poprawnie, choć nie zawsze elegancko. Prace wyglądają tak jak dziś − są pokreślone i niekiedy trudno czytelne. Nie był to jednak koniec ich zmagań z matematyką. 15 marca, w godzinach od 9 do 12:30 odbył się dodatkowy egzamin z matematyki wyższej, który zdawało już tylko dwóch spośród siedmiu maturzystów.

Bogdan: To jest własnie ten tekst, do którego link wskazał Dominik

bash: Podpowiedź do zadania od @Dominika...szukaj trójkątów podobnych

Dominik:

	8
kolejna wskazowka czy wyszlo? prawidlowa odp		.
	7

Saizou : jednak porwałem się z motyką na słońce, jutro przysiądę porządnie (mam taką nadzieję) i rozwiąże, czasami trzeba się z zadaniem przespać (ale jeśli mógłbym prosić to nie rozwiązujcie tych zadań)

Saizou :

PABP
	=?
PBCDP

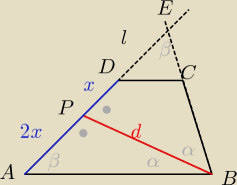
ΔCDE~ΔABE (kk)

d		d
	=
2x		x+l

x+l=2x x=l

	ΔABE		4x
k=		=		=4
	ΔCDE		x

	1
PABE=		*4x*d=2xd
	2

	1
PABP=		*2x*d=xd
	2

	2xd
42=
	PCDE

	xd
PCDE=
	8

	1		7
PBCDP=P{ABE}−PABP−PCDE=2xd−xd−		xd=		xd
	8		8

PABP		xd		8
	=		=
PBCDP		7   xd 8		7

cud że się udało

Dominik:

bezendu: @Saizou chcesz jeszcze jakieś zadanka z planimetrii

Saizou : trzeba najpierw spróbować długowiecznych zadań do Bogdana

bezendu: jak chcesz zadanka−dowody to podaj e−mail

Dominik: kolejne przyjemne (kolega mnei straszyl, ze arcytrudne − mi jakos podeszlo i od razu wpadlem na pomysl jak je zrobic): O trójkącie ABC wiadomo, że jego pole P można obliczyć następująco: P = a² − (b − c)², gdzie a, b, c oznaczają długości boków trójkąta. Wyznacz cosinus kąta leżącego naprzeciwko boku długości a.

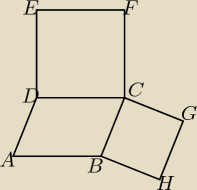
Prosiałke: Na bokach BC i CD równoległoboku ABCD zbudowano kwadraty CDEF i BCGH. Udowodnij, że |AC|=|FG|

Saizou :

	b2+c2−a2
cosα=
	2bc

Dominik: wystarczy zauwazyc, ze na bokach CF i CG mozna zbudowac przystajacy rownoleglobok do ABCD.

Dominik:

	15
Saizou, cosα =		. wskazowke?
	17

Saizou : tak łatwo się nie poddam

Saizou : na stan obecny dochodzę do momentu 4cosα=−sinα+4

Dominik: no to najtrudniejsza czesc zadania masz za soba beda 2 rozwiazania i jedno trzeba odrzucic (dlaczego?).

Saizou : bo α może należeć do I i II ćw.

Dominik: cosα = 1 ⇒ α = 0^o, dla takiego α nie ma trojkata.

Saizou : co więcej musi być to pierwsza ćwiartka, bo wyrażenie 4cosx+sinx=4 nie byłoby prawdziwe, bo gdyby α∊II ćw to 1<cos α<0 , a 1>sin>0

Dominik:

	15
a udalo ci sie dojsc do cosα =		?
	17

Saizou : jeszcze nie i na razie bark pomysłu

Dominik: podnies do kwadratu

Saizou : znaczy się postawiłem za sinx=√1−cos²x drugiej wersji nawet nie robię bo ustaliłem że x∊ I ćw.