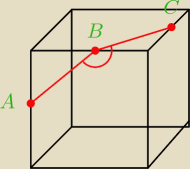
 oblicz miarę kąta między odcinkami AB i BC, jeśli punkty A, B, C są środkami krawędzi
sześcianu?
oblicz miarę kąta między odcinkami AB i BC, jeśli punkty A, B, C są środkami krawędzi
sześcianu?
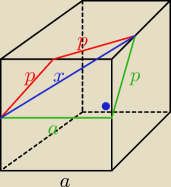
| a√2 | ||
p= | ||
| 2 |
| a√2 | 2a2 | 6 | ||||
x2=a2+( | )2=a2+ | = | a2 | |||
| 2 | 4 | 4 |
| a√6 | ||
x= | ||
| 2 |
| 6a2 | 2a2 | ||
=2* | (1−cosα) | ||
| 4 | 4 |
| 6 | |
a2=a2(1−cosα) | |
| 4 |
| 6 | 3 | |||
1−cosα= | = | |||
| 4 | 2 |
| 3 | 1 | |||
cosα=1− | =− | |||
| 2 | 2 |
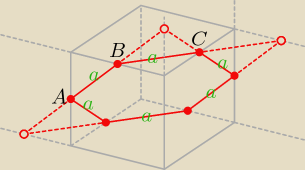 Bez obliczeń.
Przekrój sześcianu zawierający punkty A, B, C jest foremnym sześciokątem, wobec tego
miara kąta między jego bokami jest równa 120o.
Bez obliczeń.
Przekrój sześcianu zawierający punkty A, B, C jest foremnym sześciokątem, wobec tego
miara kąta między jego bokami jest równa 120o.