sinusy cosinusy tangensy akante:

	cosx
tgx+		+2=0
	1+sinx

sinx		cosx
	+		+2=0 sinx≠−1 cosx≠0
cosx		1+sinx

sinx+sin2x+cos2x
	+2=0
cosx(1+sinx)

sinx+1
	+2=0
cosx(1+sinx)

1
	+2=0
cosx

1+2cosx
	=0 ⇔ 1+2cosx=0 cosx=1/2
cosx

co źle robię? bo w odp jest −2pi/3 +2kpi i 2pi/3+2kpi

Mila: Na końcu masz błąd:

	1
powinno być: cosx=−
	2

akante: cosx rowna sie 1/2 dla pir/3 czyli −1/2 dla −pi/3?

Mila:

	1
Dla równania cos x=		masz serię rozwiązań:
	2

	π		π
x1=		+2kπ lub x2=−		+2kπ
	3		3

	1
Teraz tworzysz serię rozwiązań dla cosx=−
	2

	π		π
x1=		+π+2kπ lub x2=−		+π+2kπ
	3		3

	4π		2π
⇔x1=		+2kπ lub x2=		+2kπ
	3		3

akante: kumam to cos(pi+x)=−cosx dziękuję

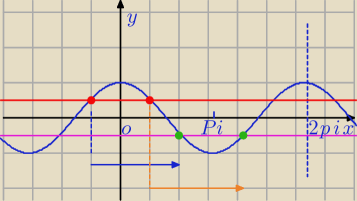
Mila: y=cosx

akante: patrz mila a jak mam równanie np −cosx=sinx to moge sobie podzielić przez cosx i wtedy powstanie tgx=−1

Mila: Możesz, zastanów się dlaczego. Teraz znikam.

akante: nie mam pojęcia dlaczego dlatego że poprostu tak się da? i to jest logiczne

akante: przeciez błedów rachunkowych nie am to chyba można czy nie?

Mila: masz równanie sinx+cosx=0 Nie wolno dzielić przez zero. Jeśli dzielisz obie strony równanie przez wyrażenie z x, to musisz mieć pewność, że jest różne od zera.

	π		π
gdyby cosx=0 to x=		a sin		=1⇔że,L≠P
	2		2

Zatem możesz przez cosx podzielić obie strony równania: sinx=−cosx