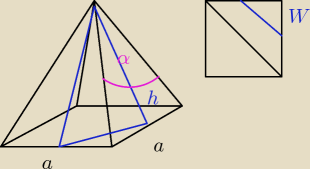
stereometria kielbasa 532 Alois~: w ostroslupie prawidłowym czworokątnym kąt sciany bocznej przy wierzchołku ostrosłupa ma miarę α. Oblicz tangens kata jaki tworzy z plaszczyzna podstawy plaszczyzna przechodzaca przez wierzcholek ostroslupa oraz srodki dwoch sasiednik bokow podstawy. liczyłam to 2 razy i wyszło mi za kazdym razem inaczej do tego nie tak jak w odpowiedzi.. i nie wiem co robie źle, moze juz rysunek skopany.. ? w= a/2 * √2 zaraz jeszcze jeden rysunek zrobię zeby nie nabazgrac

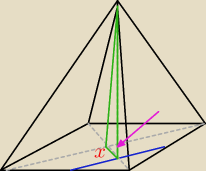Alois~: czyli tam jest ten kąt którego tg trzeba policzyc..

	1
x ma		*W .. czy ja poplątałam, liczyłam powoli dwa razy i źle.
	2

Alois~: może ktoś zerknąć chociaż na same rysunki czy poprawne ?

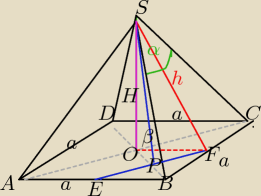Mila: ∡OPS=β− szukany tgβ

	a
|EF|=		√2
	2

	a
x=		√2
	4

Obliczyć wysokość ściany bocznej:

	α		h
ctg		=
	2		0,5a

	α
h=0,5a*ctg
	2

Z tw. Pitagorasa w ΔSOF: (OF)²+H²=h²

	1		α
(		a)2+H2=(0,5a*ctg		)2
	2		2

1		1		α
	a2+H2=		a2ctg2
4		4		2

	1		α		1
H2=		a2ctg2		−		a2
	4		2		4

	1		α
H2=		a2(ctg2		−1)
	4		2

dokończ