Rysowanie
blan: Bardzo prosze o pomoc



Zbadaj liczbę rozwiązań równania w zależności od parametru m:
|x2−6x+8|+|x2−6x+5|=m
Oczywiście rozbijam wyrażenia w modułach aby zobaczyć pierwiastki...
|(x − 4)(x − 2)| + |(x − 5)(x − 1)| = m
Zauważam jakie muszą być przedziały rozpatrywanych przypadków:
1o x∊(−
∞,1> ∪ <5,
∞) ⇒ (x − 4)(x − 2) + (x − 5)(x − 1) = m
2o x∊(1,2> ∪ <4,5) ⇒ (x − 4)(x − 2) − (x − 5)(x − 1) = m
3o x∊(2,4) ⇒ −(x − 4)(x − 2) − (x − 5)(x − 1) = m
No i teraz robię tak:
2x
2−12x+13=m
m=3
−2x
2+12x−13=m
No i teoretycznie(tak mi się wydaje..) powinienem teraz narysować te 3 funkcje z uwzględnieniem
przedziałów i napisać dla jakich m ile jest rozwiązań. Ale nie umiem tego narysować Po prostu
nie wychodzi mi, bo np ta druga funkcjia ma dwa rozw. więc przecina oś x i jest rosnąca, ale
jej wierzchołek jest w punkcie 3 no bo...
Nie wiem

coś psuje, coś robię nie tak.
Dziękuję za pomoc.
23 kwi 16:22
aniabb:
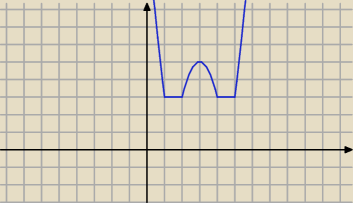
23 kwi 16:24
aniabb: dla m<3 brak rozwiązań
dla m=3 nieskończenie wiele rozwiązań
dla m∊(3;5) 4 rozwiązania
dla m=5 3 rozwiązania
dla m>5 2 rozwiązania
23 kwi 16:25
blan: ale skąd wiesz że ten wykres akurat tak wygląda
23 kwi 16:33
blan: czy możesz to jakoś bardziej mi wytumaczyć bardzo byłąm bym wdzięczna
23 kwi 16:34
blan: proszę o pomoc jeszcze raz aniu jak możesz
23 kwi 16:35
aniabb: jak rozbiłaś na przedziały to wpisz sobie nie nawiasy a takie wymnożone jak było w treści i
zobaczysz co Ci wychodzi i łatwo narysujesz
23 kwi 16:36
aniabb: ja już znikam ... ale masz praktycznie zrobione przez siebie ..tylko zamiast m wpisz y i
narysuj..a potem m odczytujesz z rysunku
23 kwi 16:37
blan: nadal nie wiem jak wymnoże te nawiasy to mi wyjdzie że
2x2−12x+13=m
m=3
−2x2+12x−13=m
a te nie mają pierwiastków całkowitych czy ktoś może mi powiedzieć
23 kwi 16:49
aniabb: ale nie szukasz pierwiastków tylko masz to narysować ..wstawiasz sobie iksy z danych
przedziałów i rysujesz i wychodzi Ci taki rysunek jak mój
24 kwi 08:33
tfghntfghfgh: αβγδπ
24 kwi 09:16
blan: a ha dziękuje już prawie złapałam
24 kwi 21:44


 Zbadaj liczbę rozwiązań równania w zależności od parametru m:
|x2−6x+8|+|x2−6x+5|=m
Oczywiście rozbijam wyrażenia w modułach aby zobaczyć pierwiastki...
|(x − 4)(x − 2)| + |(x − 5)(x − 1)| = m
Zauważam jakie muszą być przedziały rozpatrywanych przypadków:
1o x∊(−∞,1> ∪ <5,∞) ⇒ (x − 4)(x − 2) + (x − 5)(x − 1) = m
2o x∊(1,2> ∪ <4,5) ⇒ (x − 4)(x − 2) − (x − 5)(x − 1) = m
3o x∊(2,4) ⇒ −(x − 4)(x − 2) − (x − 5)(x − 1) = m
No i teraz robię tak:
2x2−12x+13=m
m=3
−2x2+12x−13=m
No i teoretycznie(tak mi się wydaje..) powinienem teraz narysować te 3 funkcje z uwzględnieniem
przedziałów i napisać dla jakich m ile jest rozwiązań. Ale nie umiem tego narysować Po prostu
nie wychodzi mi, bo np ta druga funkcjia ma dwa rozw. więc przecina oś x i jest rosnąca, ale
jej wierzchołek jest w punkcie 3 no bo...
Nie wiem
Zbadaj liczbę rozwiązań równania w zależności od parametru m:
|x2−6x+8|+|x2−6x+5|=m
Oczywiście rozbijam wyrażenia w modułach aby zobaczyć pierwiastki...
|(x − 4)(x − 2)| + |(x − 5)(x − 1)| = m
Zauważam jakie muszą być przedziały rozpatrywanych przypadków:
1o x∊(−∞,1> ∪ <5,∞) ⇒ (x − 4)(x − 2) + (x − 5)(x − 1) = m
2o x∊(1,2> ∪ <4,5) ⇒ (x − 4)(x − 2) − (x − 5)(x − 1) = m
3o x∊(2,4) ⇒ −(x − 4)(x − 2) − (x − 5)(x − 1) = m
No i teraz robię tak:
2x2−12x+13=m
m=3
−2x2+12x−13=m
No i teoretycznie(tak mi się wydaje..) powinienem teraz narysować te 3 funkcje z uwzględnieniem
przedziałów i napisać dla jakich m ile jest rozwiązań. Ale nie umiem tego narysować Po prostu
nie wychodzi mi, bo np ta druga funkcjia ma dwa rozw. więc przecina oś x i jest rosnąca, ale
jej wierzchołek jest w punkcie 3 no bo...
Nie wiem coś psuje, coś robię nie tak.
Dziękuję za pomoc.
coś psuje, coś robię nie tak.
Dziękuję za pomoc.
