aaa
:): Czy to jest dobrze?
cos(90+α)=sinα
?
23 kwi 15:18
:): Chyba znalazłem kolejny błąd w książce.
23 kwi 15:19
Dominik: dla α∊(0, 90o) cos(90o + α) = −sinα
23 kwi 15:21
xxxx:
cos(90+α) = −sinα
23 kwi 15:21
krystek: W II ćwiartce cos jest ujemny
23 kwi 15:23
xxxx:
Bardzo, ciekawe!
Dominik, a ile będzie dla α∊(900; 1500)
23 kwi 15:24
:): Ale jak? Jeśli alfa jest kątem ostrym to 90+a będzie w drugiej ćwiartce. W drugiej ćwiartce
sinus jest dodatni. Więc czemu?
23 kwi 15:24
:): Czyli mogę sobie uwzględnić minus na początku?
23 kwi 15:25
wredulus_pospolitus:
ale Ty masz cos(90+α)
... a cosx w druiej ćwiartce jest ujemny
23 kwi 15:26
krystek: Dominiku , tego zał nie musisz robić.
cos210=cos(90+120)=−sin120=−sin(90+30)=−cos30
cos210=cos(180+30)=−cos30
23 kwi 15:27
Dominik: 
racja
23 kwi 15:28
:): Dobra... W cholere z tym...
23 kwi 15:29
krystek:
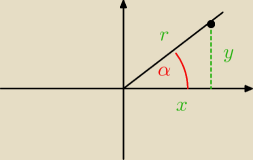
Z czym ? aby dobrze opanować znaki funkcji przedstaw je w ukł współrzędnych
| | y | | x | | y | | x | |
I teraz sinα= |
| cosα= |
| tgα= |
| ctgα= |
| i teraz w zależności w której |
| | r | | r | | x | | y | |
ćwiartce jesteś zmieniają się znaki funkcji ( r jest zawsze dodatnie
23 kwi 15:37