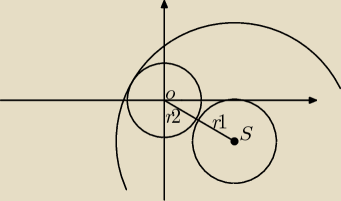
Geometria analityczna Deem: Napisz rownanie okregu o srodku S = (5, −3) stycznego do okregu o rownaniu x² +y² = 8. Na pewno rozwiazaniem bedzie (x−5)² + (y+3)², ale nie moge dojsc do tego, ile wyniesie r² w tym rownaniu [wg odpowiedzi w ksiazce r²=74]. Promien okregu o srodku w poczatku ukladu wspolrzednych ma promien r2= 2√2, a odleglosc |OS| = √34. Jezeli by wiec odjac r2 od dlugosci |OS|, wyszlo by − r1 = √32−√8, co sie nie zgadza z rozwiazaniem. Natomiast jesli by brac pod uwage okrad styczny zewnetrznie, to dlugosc jego promienia to |OS| + r2, czyli √32 + √8. Jak mam wiec to rozumiec?

wredulus_pospolitus: dwa okręgi są styczne (zewznętrznie) do siebie jeżeli: r₁+r₂ = |SO| dwa okręgi są styczne (wewnętrznie) jeżeli: |r₁−r₂| = |SO| stąd te dwa przypadki

Deem: Natomiast jesli by brac pod uwage okrad styczny wewnetrznie* Mala poprawka

wredulus_pospolitus: zamień √32 i √8 na ładniejsze liczby

Deem: Znowuz blad, przepraszam. Na poczatku napisalem |OS| − √34 i tyle wlasnie on wynosi.

Deem: W rownaniu okregu prawa strona to r², wiec wychodzi i tak albo 34+8, albo 34−8, a to sie nie zgadza z rozwiazaniem podanym w odpowiedziach, czyli 74.

wredulus_pospolitus: niee wychodzi r = √34 + √8 lub r= √34 − √8 czyli: r² = ... lub r² = ...

aniabb: https://matematykaszkolna.pl/strona/3254.html

Deem: r² = 42 + 8√17 ≈ 74 lub r² = 42 − 8√17 ≈ 10 teraz dopiero zauwazylem, ale znowu poleglem z pierwiastkami, da sie cos z tym zrobic, by wynik byl dokladny?

wredulus_pospolitus: nie ... niestety nie da się