pomocy kaśka: W ostrosłup prawidłowy czworokątny wpisano sześcian o krawędzi 6 w taki sposób że cztery wierzchołki sześcianu należą do krawędzi bocznych ostrosłupa, a pozostałe cztery do jego podstawy. Ściana boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30◯.oblicz pole powierzchni tego ostrosłupa. wychodzi mi 756 + 456 √3 a powinno być 756+300√3 pomozcie!

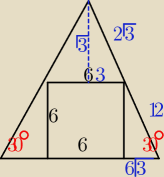
aniabb: Pp= (6+12√3)²= 36+144√3+432=468+144√3 Pb=4•(6+12√3)•(12+2√3)/2 = 2•(72+12√3+144√3+72) = 288+312√3 całość 756+456√3 no nie chce być inaczej

kaśka: ok, dzięki

Myron: W obliczeniu Pb jest błąd, w drugim nawiasie powinno być (6+√3) i wtedy wynik to: 612+300√3.

Weronika: Dobrze jest. Do pola bocznego bierzemy wysokość ściany bocznej czyli (12 + 2√3); obliczamy pole trójkąta ( ściany bocznej ) i mnożymy x4.