aaa :):

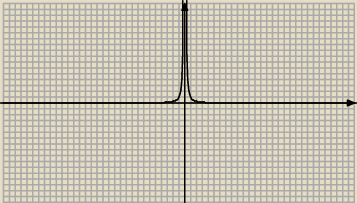
	1
Na rysunku obok przedstawiono wykres funkcji f(x)=		. Prosta równoległa do osi OX
	x2

przecięła wykres funkcji w punktach A i B. Wykaż, że pole trójkąta ABC, gdzie C(3,−1), jest większe lub równe 2. Nienawidzę niczego wykazywać. NIe umiem się do tego zabrać.

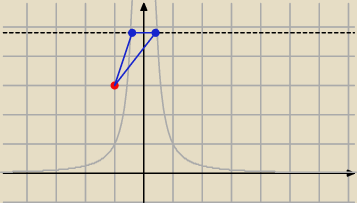
Artur_z_miasta_Neptuna: przeczytaj treść jeszcze raz ... o czymś (co do tej prostej) zapomniałeś/−aś napisać jeżeli nienawidzisz wykazywać ... to znaczy, że niestety − matematyka to dla Ciebie coś co robisz 'automatycznie' (jak np. podawanie faktów historycznych)

:): Owszem, robie dużo rzeczy automatycznie, lecz to tez nie oznacza, że nie myślę. Po prostu mi to nie idzie. Z nauczycielką robilismy może kilka zadań z wykaż, że w ciągu 3lat. I te zadania były banalne (jak dla mnie). Więc powiedzmy, że nie nauczyłem się od niej jak wykazywać trudniejsze przykłady. Jest wiele takich osób jak ja i czuję się mocno urażony Twoimi słowami, bo odbieram to jakby nie była dla mnie. Wracając do zadania. Podałem wszystko to co było w treści.

:): *bo odbieram to jakby matematyka nie była dla mnie.

Artur_z_miasta_Neptuna: jeżeli podałeś wszystko ... to nie jest to prawdą: przykład: C=(3,−1)

	1
A=(−10 ;		)
	100

	1
B = (10 ;		)
	100

	1		1
PABC =		*(20*(3−		) > 20 >> 2
	2		100

brakuje warunku, że ów prosta nie może być niżej jak y=1 ... czyli musi zachodzi y≥1 a jak wtedy to udowodnić niech y=m: h trójkąta = |m−3|

	1
'a' trójkąta = 2*
	m2

1^o m∊<1;3)

	1		2		3−m		3−1
P =		*(3−m)*		=		≤ (funkcja malejąca na tym przedziale)		=2
	2		m2		m2		12

2^o m∊(3;+∞)

1

2

m−3

1 − 1/m

1 − 0

1

1

P =

*(m−3)*

=

=

>

=

≥

>2

2

m2

m2

m

m

m

3

c.n.w.

:): Teraz sam doszedłem do wniosku, że pkt A(−x,y), B(x,y) Zaznaczyłem sobie to na wykresie. I powstał mi jakiś trójkąt ABC. |AB|= 2x h = y+1

1
	*2x+(y+1)≥2
2

Po przekształceniu doszedłem do takiej formy.

	2
y≥
	x+1

:): I jak tą formę rozwiązać?

Artur_z_miasta_Neptuna: ehhh ... źle zaznaczyłem punkt C a Ty źle przekształciłeś:

1
	2x*(y+1) ≥2
2

x*(y+1) ≥2

	2
y+1 ≥		(przy założeniu x>0 ... które bez problemu można poczynić)
	x

	2
y ≥		−1
	x

	2−x
y ≥
	x

	1
a wiemy, że y=
	x2

stąd:

1		2−x
	≥
x2		x

1− (2−x)*x
	≥ 0
x2

patrzymy na licznik (bo mianownik >0) 1 − 2x + x² ≥ 0 (1−x)² ≥ 0 spełnione dla każdego 'x' c.n.w.

:): Oki. Dziękuję.

asdf: znam dobry patent − zrób tak z 50 zadań tego typu, mi pomogło