 gdzie tu jest bład?
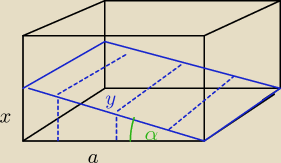
gdzie tu jest bład?  Sześcian podzielono płaszczyzną przechodzącą przez krawędź podstawy na dwie bryły z których
jedna ma pięć, a druga sześć ścian. Pole powierzchni całkowitej tej bryły, która ma pięć ścian
jest równe połowie pola powierzchni sześcianu. Oblicz tangens kąta nachylenia płaszczyzny
dzielącej sześcian do płaszczyzny podstawy.
Ps =6a2
P1= 1/2 * 6a2 = 3a 2
xa+ay+a2+xa=3a2
Sześcian podzielono płaszczyzną przechodzącą przez krawędź podstawy na dwie bryły z których
jedna ma pięć, a druga sześć ścian. Pole powierzchni całkowitej tej bryły, która ma pięć ścian
jest równe połowie pola powierzchni sześcianu. Oblicz tangens kąta nachylenia płaszczyzny
dzielącej sześcian do płaszczyzny podstawy.
Ps =6a2
P1= 1/2 * 6a2 = 3a 2
xa+ay+a2+xa=3a2
| x | ||
wyznaczyłam | = tgα => x=a tgα | |
| a |
| a | a | ||
= cosα => y = | |||
| y | cosα |
| 1 | ||
cosα−sinα = | ||
| 2 |
| sinα | ||
tgα = |  | |
| 1/2 + sinα |
 ?
tak mało czasu do matury :<
?
tak mało czasu do matury :<
| 1 | ||
cosα − sinα = | /()2 | |
| 2 |
| 1 | ||
cos2α−2sinαcosα+sin2α = | ||
| 4 |
| 1 | ||
1−2sinαcosα = | ||
| 4 |
| 1 | ||
1−sin(2α) = | ||
| 4 |
| 3 | ||
−sin(2α) = − | ||
| 4 |
| 3 | ||
sin(2α) = | ||
| 4 |
| √7 | ||
cos(2α) = | ||
| 4 |
| 3 | ||
tg(2α) = | ||
| √7 |
| 2tgα | ||
tg(2α) = | ||
| 1−tg2α |
| 2tgα | 3 | ||
= | |||
| 1−tg2α | √7 |
| −2√7−8 | ||
tgα = | < 0 odpada bo α ∊(0;45) | |
| 6 |
| −2√7+8 | −√7+4 | |||
tgα = | = | |||
| 6 | 3 |
| x | ||
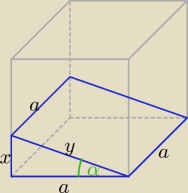
α∊(0, 45o) tgα = | = k∊(0, 1), y = √a2 + x2 | |
| a |
| 1 | ||
2* | ax + ax + a2 + a√a2 + x2 = 3a2 /:a ⇒ √a2 + x2 = 2a − 2x /2 | |
| 2 |
 cosα=1/2+sinα
podstawiam do jedynki
sin2α +sinα − 3/4 = 0
Δ=4
sinα= −3/2 −− czyli odpada
sinα=1/2
czyli by był.. cosα=1
czyli tgα= 1/2 czyli takim sposobem nie wolno
cosα=1/2+sinα
podstawiam do jedynki
sin2α +sinα − 3/4 = 0
Δ=4
sinα= −3/2 −− czyli odpada
sinα=1/2
czyli by był.. cosα=1
czyli tgα= 1/2 czyli takim sposobem nie wolno  ?
?
 moze tym mi wyjdzie
moze tym mi wyjdzie
 bo ujemna delta, to musze ogarnąć ten sposób Twój Basiu
bo ujemna delta, to musze ogarnąć ten sposób Twój Basiu 
| 8 − 2√7 | 4 − √7 | 8 + 2√7 | 4 + √7 | |||||
k = | = | lub k = | = | > 1 odpada | ||||
| 6 | 3 | 6 | 3 |
| 4 − √7 | ||
Odp.: tgα = | ||
| 3 |