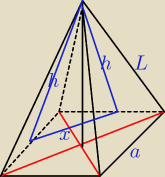
Gdzieś popełniam błąd i nie mogę się połapać sos: Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe P, a kąt między wysokościami jego dwóch sąsiednich ścian bocznych wychodzącymi z wierzchołka ostrosłupa jest równy 2α. Oblicz długość krawędzi podstawy i wysokość ostrosłupa

Basia: P = 4*¹₂*a*h = 2ah

	P
h =
	2a

spodki wysokości są w połowie krawędzi stąd

	a2		a2		2a2
x2 = (a2)2+(a2)2 =		+		=
	4		4		4

	a√2
x =
	2

	x2
sinα =
	h

	a√2
h*sinα = x2 =
	4

P*sinα		a√2
	=
2a		4

	2a2√2		a2√2
P*sinα =		=
	4		2

	2P*sinα
a2 =		= P*√2*sinα
	√2

a = √P*√2*sinα czy dotąd jest dobrze ? sprawdź wynik, bo paskudny wyszedł

Arlekin: Mi wyszło a takie samo, H natomiast jeszcze brzydsze.

	√√2sinαP√2cos2α
H=
	4sinα