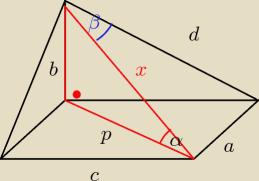
 Jedna z krawędzi bocznych ostrosłupa, którego podstawą jest prostokąt, ma długość b
i jest prostopadła do płaszczyzny podstawy.
Najdłuższa krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze α , a z jedną z sąsiednich
krawędzi bocznych kąt β. Wyznacz objętość ostrosłupa.
nie wiem czy dobrze zaznaczyłam ten β, zaczelam robic wiem tylko że
Jedna z krawędzi bocznych ostrosłupa, którego podstawą jest prostokąt, ma długość b
i jest prostopadła do płaszczyzny podstawy.
Najdłuższa krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze α , a z jedną z sąsiednich
krawędzi bocznych kąt β. Wyznacz objętość ostrosłupa.
nie wiem czy dobrze zaznaczyłam ten β, zaczelam robic wiem tylko że
| b | ||
x = | ||
| sinα |

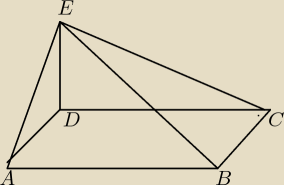 ΔBCE jest prostokątny
ΔBCE jest prostokątny
| b | ||
x= | ||
| sinα |
| b | ||
1) tgα= | ⇔b=p*tgα⇔p=b*ctgα | |
| p |
| a | b | |||
sinβ= | ⇔a=x*sinβ⇔a= | *sinβ | ||
| x | sinα |
| b | ||
c2=(b*ctgα)2−( | *sinβ)2 | |
| sinα |
 jutro w dzień zajrze
jutro w dzień zajrze