równanie Maciej: x³+5x²+3x−15=0 x²(x+5)+3(x−5) (x²+3) (x+5)(x−5) ↙ ↓ ↘ x₁=−3 x₂=−5 x₃=5 Czy dobrze zrobilem?

asdf: 1. W pierwszej linijce masz równość ⇒ przyrównujesz do zera..w kolejnych już tego nie robisz 2. x² + 3 = 0 ⇒ Δ < 0 Staraj sie to robić ze zrozumieniem..

Maciej: ale wynik jest dobry?

asdf: nie, zły w jednym przypadku, czemu sie pytasz czy wynik dobry jak Ci napisałem, że: x² + 3 = 0, czyli to nie ma miejsc zerowych. Narysuj sobie funkcje i o ile nie zaszkodzi − zacznij myśleć

Maciej: x₁=0?

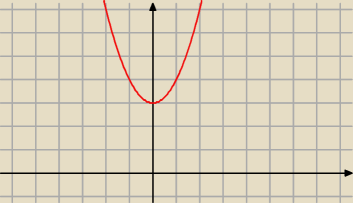
asdf: widzisz gdzieś w tej funkcji miejsce zerowe? na wykresie: y=x²+3

Maciej: czyli pod x₁ mogę napisać nie ma?

asdf: powinieneś

ICSP: w ogóle to zrobiłeś z wielomianu stopnia III wielomian stopnia IV całość do poprawki

Maciej: to jak to powinno być?

asdf: dokładnie, nie zauważyłem, skupilem sie na błędzie: x²+3 = 0 ⇒ x = −3 (co jest totalną bzdurą) x³+5x²+3x−15=0 x³ + 5x² + 3x − 15 = 0 x(x² + 3) + 5(x² − 3) = 0 ...to już ciężko rozwiązać, http://www.wolframalpha.com/input/?i=x%5E3%2B5x%5E2%2B3x%E2%88%9215%3D0 to nie powinno być tak?: x³ + 5x² − 3x − 15 = 0

Maciej: i co kolejne miejsca zerowe to x1 nie ma x2 to 3 i x3 to−3

asdf: jakbym Cie zrozumiał to bym Ci pomógł

ICSP: asdf chodzi o to żę źle przepisałeś przykład. Gdzieś zamiast − powinien być + albo na odwrót

Maciej: −x²+5x²+3x−15= 0 prawidłowy

asdf: to ja źle przepisałem przykład? poddaje się..do widzenia Maćku.

Maciej: −x2+5x2+3x−15= 0

ICSP: [Casdf]]'owi No już się ie gniewaj Czyli teraz x³ zamieniło się w x²

Maciej: Przepraszam cos mi sie tu z tymi potegami myli

ICSP: widać −x³ + 5x² + 3x − 15 = 0 najpierw dzielę przez (−1) aby mieć znaczek + przy najwyższej potędze x³ − 5x² −3x + 15 = 0 x²(x−5) − 3(x−5) = 0 (x−5)(x² − 3) = 0 (x−5)(x−√3)(x+√3) = 0 x = 5 v x = ±v √3

Maciej: dzieki