długośc ramion w trapezie w ukł. wspołrzędnych Ola: Proste k i l są równoległe do osi OX i przecinają wykres funkcji ⁻⁴_|x| odpowiednio w punktach A,B i C,D w ten sposób, że czworokąt ABCD jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu. narysowałam wykres, wypisałam wzory prostych, mam ew. wygląd punktów A,B, C,D. i udało mi się tylko dojść do tego że a+b=6 więc do obwodu potrzeba mi jeszcze ramion, i nie mam pomysłu jak je wyliczyć Jakieś sugestie ?

czarek:

(a+b)*h
	=6 ⇒a+b=6
2

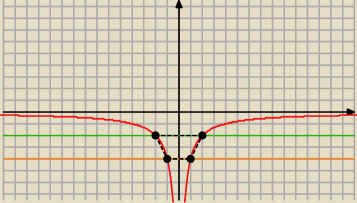
a+b=2c 6=2c c=3 obw=6+6=12 mogę się mylić

Eta: Ob= 6+2√5

yroz: Wie ktoś jak to rozwiązać ?

Wallach: a+b=6 A=(−x; f(− x ))=(−x ; −4/x) B=(x; f(x)) = (x; −4/x) zatem: |AB|=a=√(x−(−x))² + (−4/x + 4/x))²=2x C=(x₁; f(x₁)) = (x₁; −4/x₁) = (x₁; −4/x + 2) [przyp. odległość między odcinkami wynosi h=2, zatem f(x₁) = f(x) + 2] D=(−x₁; f(−x₁)) = (−x₁; −4/x₁) |CD| = 2x₁ f(x₁) = f(x) + 2 −4/x₁=−4/x + 2 po przekształceniu x₁=4x/(4−2x) |CD|=b=2 * 4x/(4−2x)= 8x/(4−2x) Wracamy do a+b=6 i rozwiązujemy równanie kwadratowe pamiętając o założeniach. [a,b∊(0;6)]

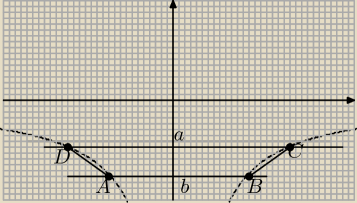
Arek: Witam, proszę o sprawdzenie A=(Xa, −4/Xa) D=(Xd, −4/Xd) a − 2Xd, b − 2Xa Układ: 2Xd+2Xa = 6 /:2 −4/Xa − (−4/Xd) = 2 /* wysokość trapezu = 2, więc Ya−Yd=2 */ Po przekształceniu: Xa²+Xa−6=0 Delta = 25 Xa = −3 ⋁ Xa'= 2 Xd = 6 ⋁ Xd'= 1 A=(−3, −4/3), D=(6, −2/3) ⋁ A'=(2,−2), D=(1,−4) |A'D'| = √5 więc L= 6+2*√5 I tu pojawia się moje pytanie, mianowicie, dlaczego drugi wynik jest niezgody z rozwiązaniem? Bo Xa ⋀ Xd powinny być mniejsze od zera (tak jak na rysunku)?

MAturzysta :): skąd wzięło się to ,,po przekształceniu: xa² xa − 6 = 0 ? Bo nie mogę wykminić?