pole trójkąta
~pati~: W trójkącie prostokątnym ABC cosinus kąta ABC wynosi 0,8. W trójkąt wpisano okrąg, punkt D jest
punktem styczności tego okręgu z przeciwprostokątną AB. Wiedząc, że promień tego okręgu jest
równy 5 cm, oblicz pola trójkątów ADC i DBC.
21 kwi 20:35
Artur_z_miasta_Neptuna:
masz wartość cosinusa −> masz proporcję boków tego trójkąta ... do dzieła
21 kwi 20:36
~pati~:
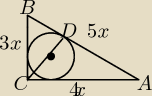
no ok mam proporcję czyli będzie tak
i co z tym dalej?
21 kwi 20:52
Janek191:
Do tego rysunku :
P = 0,5 *4 x* 3 x = 6 x2
oraz
P = 0,5 *r*( 3x + 4x + 5x) = 0,5*5 *12 x = 30 x
zatem
6 x2 = 30 x
6 x2 − 30 x = 0
6 x*( x − 5 ) = 0
x = 0 lub x = 5, ale x musi być > 0, zatem
x = 5
−−−−−−−
Mamy :
I AB I = 25 cm
I AC I = 20 cm
I BC I = 15 cm
Niech I CD I = y oraz I BD I = z
zatem
152 = y2 + z2
y2 + ( 25 − z )2 = 202
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
y2 = 225 − z2
y2 + 625 − 50 z + z2 = 400
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
225 − z2 + 625 − 50 z + z2 = 400
− 50 z + 850 = 400
50 z = 450
z = 9
−−−−−−−
y2 = 225 − 92 = 225 − 81 = 144
y = 12
−−−−−−−
Mamy więc
y = I CD I = 12 cm
z = I BD I = 9 cm
oraz
PΔ ADC = 0,5 *y* ( 25 − z) = 0,5*12*16 = 96
PΔ DBC = 0,5 *y*z = 0,5*12*9 = 54
Odp. PΔ ADC = 96 cm2, a PΔ DBC = 54 cm2
==========================================
22 kwi 10:07
Guć: eee. zadanie żle zrobione powinny wyjść takie pola = 60 i 90 .
4 cze 16:31
Eta:
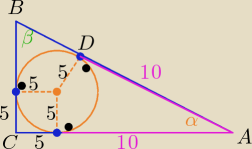
Z obliczeń podanych przez
Janek191 powinno być:
|AC|= 15 , |AB|= 25, |BC|=20
bo |AC|= 3x , |BC|= 4x , |AB|= 5x skoro cos(<ABC)= 0,8
| | 4x*3x | | 3x+4x+5x | |
P(ABC)= |
| = 6x2 i P(ABC)= |
| *r = 30x |
| | 2 | | 2 | |
to 6x
2=30x⇒
x=5
zatem:
P(ABC)= 150 cm
2
| | 1 | | 1 | |
cosβ= sinα= 0,8 to P(ADC)= |
| *|AC|*|AD|*sinα= |
| 15*8=60 cm2 |
| | 2 | | 2 | |
to P(BCD)= 150−60=
90 cm
2
4 cze 23:05
fgdfg: αααα
3 paź 23:18
gosc: czemu janek191 ma zły wynik? wytłumaczy ktoś, bo rozumiem oba sposoby i wydają się oba okej ale
jednak wynik inny wychodzi...
30 maj 10:01
Jack: Wydaje mi sie ze blad jest w zalozeniu − mianowicie, ze |CD| = y wcale nie jest pod katem
prostym do BD.
promien jest jak najbardziej pod katem prostym, ale y juz nie koniecznie.
http://puu.sh/pa5Be/f546a19a1c.png
30 maj 10:46
GÓWNO: β≤≥
30 maj 10:55
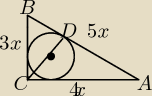 no ok mam proporcję czyli będzie tak
i co z tym dalej?
no ok mam proporcję czyli będzie tak
i co z tym dalej?
 Z obliczeń podanych przez Janek191 powinno być:
|AC|= 15 , |AB|= 25, |BC|=20
bo |AC|= 3x , |BC|= 4x , |AB|= 5x skoro cos(<ABC)= 0,8
Z obliczeń podanych przez Janek191 powinno być:
|AC|= 15 , |AB|= 25, |BC|=20
bo |AC|= 3x , |BC|= 4x , |AB|= 5x skoro cos(<ABC)= 0,8