Dziwne ze stożkiem MM: Trójkąt o bokach 2,3,4 obraca się wokół najdłuższego boku. Oblicz objętość bryły powstałej w wyniku tego obrotu.

pytajka: Dostaniesz dwa stożki. Jeden o tworzącej 3 i drugi 2. Wysokość jednego to x, drugiego 4−x. Promień to wysokość podanego trójkąta padająca na bok równy 4. Oznacz w trójkącie tę wysokość i z dwóch twierdzeń Pitagorasa dostaniesz układ równań: h² + x² = 2² h² + (4−x)² = 3² Chyba dalej łatwo, ale niech ktoś mnie sprawdzi, bo tak na szybko.

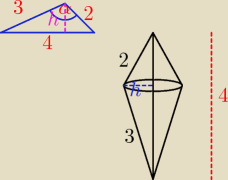
Tomek: w wyniku obrotu powstają dwa stożki o tych samych podstawach. aby obliczyc ich V musimy znależć wysokość trójkąta opuszczoną na podstawe o dł 4 (h=r) z tw kosinusów liczymy α: 16=9+4−2*2*3*cosα

	1
cosα=−		− a więc II ćwiartka (kąt 90<α<180)
	4

z jedynki trygon. liczymy sinα: sin²α=1−cos²α

	√15
sinα=		ujemny sinus odrzucamy bo musi byc dodatni
	4

liczymy pole trójkąta ze wzoru:

	2*3*sinα		3√15
P=		=
	2		4

obliczamy teraz h:

	4*h
P=		=2h
	2

	3√15
2h=
	4

	3√15
h=
	8

teraz podstawiamy na wzór V:

	1		3√15		45
V=		*π*(		)2*4=		π
	3		8		16

powinno być dobrze...

Brunetka94: x+y=4 2² = r² + x² ⇒ r² =4−x² 3²= r² + y² ⇒ 9 − y²

⎧	x+y=4⇒4−y
⎩	4−x2=9−y2

4−16 + 8y −y² = 9−y² 8y=21 y=²¹₈ x= 4 − ²¹₈ = ¹¹₈ r= √4−x² = √4−¹²¹₆₄ = ⁴⁵₁₆ pi H1 = x = ¹¹₈ H2 = y = ²¹₈ H1 + H2 = 4 r = ^3√15₈ Vc = V1 + V2 = ⁴⁵₁₆ pi