Proszę pomóżcie Tomasz: W trójkącie prostokątnym ABC cosinus kąta ABC wynosi 0,8. W trójkąt wpisano okrąg; punkt D jest punktem styczności tego okręgu z przeciwprostokątną AB. Wiedząc, że promień okręgu jest równy 5 cm, oblicz pola trójkątów ADC i DBC.

irena_1:

	a
cosα=0,8=
	c

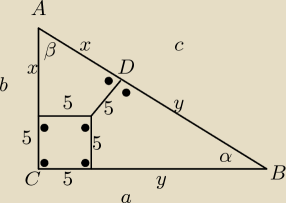
a=0,8c a+b=c+2r 0,8c+b=c+10 b=0,2c+10 (0,8c)²+(0,2c+10)²=c² 0,64c²+0,04c²+4c+100=c² −0,32c²+4c+100=0 −0,08c²+c+25=0 /*(−25) 2c²−25c−625=0 Δ=625+5000=5625

	25−75		25+75
c1=		<0 lub c2=		=25
	4		4

c=25 a=0,8*25=20 b=0,2*25+10=15 x=b−5=10 y=a−5=15 cosα=0,8 sin²α=1−0,8²=1−0,64=0,36 sinα=0,6

	1
PBCD=		*20*15*0,6=90
	2

sinβ=cosα=0,8

	1
PACD=		*15*10*0,8=60
	2

Tomasz: 2c2−25c−625=0 Δ=625+5000=5625 c1<0 lub c2=25 c=25 nie rozumiem jak do tego doszłaś, że c=25

irena_1: Bo c to długość odcinka, więc nie może być ujemna