Dominik: jak mozna wykazac, ze jesli w rownoleglobok wpiszemy romb (tak ze boki rombu sa rownolegle do przekatnych rownolegloboku) to przekatne rownolegloboku dziela boki rombu na polowy?

Dominik: podbijam

:):

:): Jakoś tak. A potem udowodnij to kątami. Oznacz sobie α i β.

:): A sory. równoległobok w romb. xD

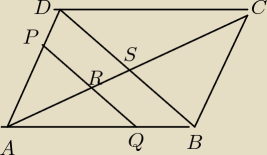
PW: Z twierdzenia Talesa wynika

PQ		AQ
	=
DB		AB

RQ		AQ
	=
SB		AB

skąd

PQ		RQ
	=
DB		SB

Ponieważ przekątne równoległoboku połowią się, po oznaczeniu DB=d₁ mamy

PQ		RQ
	=		,
d1		d1   2

skąd PQ=2RQ. Widać, że wspomniany podział na pół wynika jedynie z tego, że PQ jest równoległy do BD (nie ma to bezpośredniego związku z tym, że wpisany czworokąt jest rombem). Kreski oznaczające długości odcinków pominąłem dla szybkości zapisu.

Dominik: dzieki!