Trójkąty Poranny ptaszek: W trójkącie prostokątnym punkt styczności okręgu wpisnego w ten trójkat dzieli przeciwprostokątną na odcinki długości 5 i 12 cm . Oblicz dłgość przyprostokątnych trójkąta. Prosiłbym o rysunek

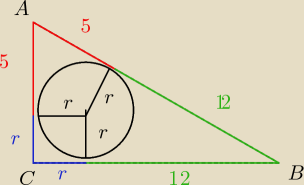
Edek: (r+5)²+(r+12)²=17² oblicz r i wyznacz boki

Poranny ptaszek: Dzięki, rysunek wiele wyjąsnia.

misiu: te równanie obliczyć za pomocą wzoru skróconego mnożenia?

Bogdan: To równanie trzeba rozwiązać (nie obliczyć) stosując po drodze wzory skróconego mnożenia.

Poranny ptaszek: Doszedłem do 2r² + 34r = 120 i nie wiem jak to gryźć dalej ...

misiu: doszedłem do tego samego momentu i nie wiem co dalej

Bogdan: Najpierw uprościmy równanie dzieląc je przez 2: r² + 17r = 60 ⇒ r² + 17r − 60 = 0 i r > 0, teraz Δ.

misiu: Δ=b²−4ac Δ=289−240 Δ=49 √Δ=7 czy r (promień) wynosi 7 ?

Bogdan: Nie

Poranny ptaszek: Tam powinien byc plus Δ=289+240

Poranny ptaszek: Δ=289 − 4 * 1 * (−60) Δ=289+240 Δ=529 √Δ = 23

Bogdan: Teraz dobrze, a więc r = ....

Poranny ptaszek: x1 = −20 x2 = 3 i co dalej ?

Bogdan: nie x₁ i x₂, ale r₁ i r₂, wiemy, że r > 0, więc wartość ujemną trzeba odrzucić.

Bogdan: |AC| = 5 + r, |AB| = 17, |BC| = 12 + r

Poranny ptaszek: Do czego będzie potrzebna nam Δ ?

misiu: nie Δ tylko √Δ zeby wyliczyc r1 i r2 r1 wtedy wyjdzie −20 a r2 3 wtedy r1 odrzucamy bo < 0 wiec zostaje 3 jak dodasz to ci wyjdzie ze przyprostokątne maja 8 i 15 cm

Poranny ptaszek: aaaaaaaaaaaa to zamiast x1 jest r1, prosta zamiana. Wszystko wiadomo.

Poranny ptaszek: Siatka o długści 300m stanowi ogrodzenie działki o kształcie prostokąta. Jakie są wymiary tej działki jeżeli wiadomo, że ma ona najwięszke z mozliwych pole powierzchni. Wydaje mi sie ze zadanie okaze sie jak zawsze łatwe ale ja nie mam pomysu jak to zacząc. Prosze jeszcze raz o pomoc.

Poranny ptaszek: Pomoże ktos ?

Bogdan: 2x + 2y = 300 ⇒ x + y = 150 ⇒ y = 150 − x P = xy → max P = x*(150 − x) Funkcja P(x) = −x² + 150x jest funkcją kwadratową posiadającą maksimum

	−150
dla x =		= 75
	−2

y = 150 − 75 = 75. Działka jest kwadratem o boku 75.

Poranny ptaszek: −150 dla x = −−−−−− = 75 −2 wytłumacz mi dokładnie skąd to sie wzieło, znaczy dlaczego to podzieliłes ?

Poranny ptaszek: i czy to jest jedyny sposob rozwiązania zadania ?

Poranny ptaszek: Moze podstawiłes to do jakiegos wzoru, mógłbys mi go tutaj napisac ?