pytanie denatlu: Czy przekątne równoległoboku zawsze dzielą go na cztery trójkąty o równych polach?

Saizou : tak

Bogdan: Proponuję to wykazać w jak najprostszy sposób.

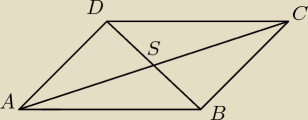
Saizou : ΔABS=ΔBCS=ΔBDS=ΔADS, z cechy przystawania trójkątów bok,kąt bok coś takiego

Bogdan: A co oznacza zapis ΔABS = ΔBCS ?

Saizou : nie mogłem znaleźć znaku przystawania trójkątów

Bogdan: Jeśli |AB| ≠ |BC| to trójkąty ABS i BCS nie są przystajace

Mila: Oj, Saizou, popraw się.

Saizou : no to będzie: ΔABC=ΔABC (bo moją tę samą wysokość i podstawę lABl) ΔABS+ΔADS=ΔABS+ΔBCS ΔADS=ΔBCS

Saizou : (bo mają...)

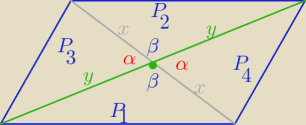
Eta: β= 180^o−α , sinβ= sinα

	x*y
P1=P2=P3=P4=		*sinα
	2

Bogdan: ΔABC = ΔABC to oczywiście oczywista oczywistość ΔABS + ΔADS a co to oznacza?

Saizou : chodziło o pola , które zostały pożarte w bliżej nieokreślonych warunkach

PW: Poprowadzić wysokość h zawierającą punkt S, wtedy widać, że suma pól trójkątów ABS i CDS jest

	1		h		1
równa		(|AB|+|CD|)		=		|AB|h (skorzystaliśmy z równości długości boków AB i
	2		2		2

CD). Oznacza to, że suma pól tych trójkątów jest połową pola równoległoboku, a ponieważ trójkąty sa

	1
przystające, każdy z nich ma pole równe		pola równoległoboku.
	4

Trójkąty BCS i DAS też są przystające i sumę pól mają równą połowie pola równoległoboku, więc

	1
ich pola też są równe		pola równoległoboku.
	4

Eta: Ejj Saizou "posil się" ...

Bogdan:

PW: Eta, dla siebie też bym tak zrobił, ale Bogdan zadał warunek "w jak najprostszy sposób", więc udawałem, że tego wzoru nie znam.

Saizou : mniam, mniam, zdrowe jabłuszko zawsze pomoże dzięki Eto, a w zamian nasz wyhodowany na przydomowym ogródku

Eta:

Saizou : w jak najszybszy sposób: "bo tak" cnu

denatlu: dzięki