Okręgi przecinające się pasażer: Mam teoretyczne pytanie. Czy, jeżeli okręgi przecinają się w dwóch punktach, to prosta łącząca środki tych okręgów będzie prostopadła do prostej łączącej punkty wspólne tych okręgów? Co w rezultacie utworzy nam piekny deltoid ?

pasażer: pomoże ktoś? :c Może wytłumaczę, po co mi to. Mam dane dwa równania okręgów x²+y²=625 i (x−36)²+(y−15)²=1600 i mam powiedziane że przecinają się w punkcie A i B i mam odległość dwóch tych punktów obliczyć. Stwierdziłam, że zmaganie się z tymi dwoma okręgami w układzie równań to katorga i na bank się pomylę parę razy znając mnie. Więc obliczyłam odległość środków |S₁S₂|=39 i z twierdzenia cosinusów obliczyłam cosα pomiędzy dwoma promieniami z trójkąta 25,40,39. Zamieniłam na sinα i dwa razy z wzoru na pole obliczyłam wysokość, która (wg. moich założeń) równa 1/2 odległości |AB|. Wysokość trójkątów S₁AS₂ ( i S₁BS₂) równa się 24. Wynik: 48. Dobrze?

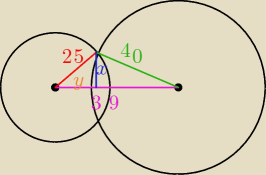
Aga1.: Nie wiem czy szybciej, ale rozwiązałam z układu równań i wynik jest taki sam. x²+y²=25² x²+(39−y)²=40²

pasażer: Świetny pomysł Aga1. Tylko wtedy też zakładasz, że x jest prostopadłe do y. Widocznie tak jest, dziękuję!