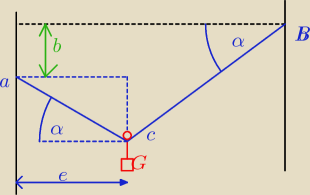
Geometria Miraclepl: Geometria − skąd wzięło się to rozwiązanie? Witam, nie chce wnikać w to, że to jest zadanie z mechaniki, chodzi mi tylko i wyłącznie o wytłumaczenie rozwiązania, które opiera się tylko i wyłącznie na geometrii.(obrazek) Treść: Line AB o długości l zawieszono miedzy dwiema pionowymi ścianami oddalonymi od siebie o a, przy czym koniec B zawieszono o b wyżej od końca A, Na linie umieszczono krążek obciążony ciałem o ciężarze G. Ustalić położenie równowagi oraz naciąg liny. ODP: krążek ustawia się tak aby obie części liny tworzyły z poziomem jednakowe kąty. i tu jest podane:

	a		G		1
cosα=		, S=		i e=		(lcosα−bctgα) (właśnie tej ostatniej odpowiedzi na e
	l		2sinα		2

nie rozumiem − skąd to się wzięło? . Z góry dziękuję za wszelką pomoc

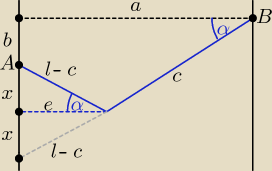
Bogdan: Może taki rysunek pomoże.

Miraclepl: Może trochę niefortunnie oznaczylem na rysunku ABC to są punkty na linie. Natomiast b i e (z malej litery) to odległości. Ty tutaj oznaczyles w paru miejscach c a takiej wartosci nie mam podanej. Powiem szczerze dalej nie widzę skąd autor ksiazki wyprowadził e

Bogdan: To wykonaj rysunek fortunnie

Miraclepl: http://imageshack.us/photo/my-images/818/img20130420195703.jpg Prosze bardzo ,mam nadzieje ze sie wyswietla.

Bogdan: Nie wyświetla się. Wpisałem c tam gdzie Ty. Podaj, co masz dane patrzą na mój rysunek.

Miraclepl: http://img818.imageshack.us/img818/1356/img20130420195703.jpg Ten powinien dzialac. Podane mam tylko to co w tresci zadania.

Bogdan: Podaj jeszcze raz wzór na e, w Twoim zapisie w tym wzorze występuje c, którego nie ma na rysunku

Miraclepl: Tam jest cotangens (ctg) α, tam żadnego c nie ma

Bogdan: Zapis bctgα można zrozumieć jako b*c*tgα (i tak to przeczytałem) albo b*ctgα. Gdybyś rysunek i zapis zadania wykonał w sposób nie budzący wątpliwości, to wskazówki otrzymałbyś zdecydowanie szybciej. Bierzemy mój rysunek.

a		e		e
	= cosα ⇒ a = l*cosα,		= ctgα ⇒ x =
l		x		ctgα

a		e
	= ctgα ⇒ a = b*ctgα + 2x*ctgα ⇒ a = b*ctgα + 2*		*ctgα
b + 2x		ctgα

	a − b*ctgα		l*cosα − b*ctgα
a = b*ctgα + 2e ⇒ e =		=
	2		2

Miraclepl: Dziękuję Bogdan i przepraszam za nieścisłości! Pozdrawiam

Bogdan: