stereometria waluś: Podstawą graniastosłupa prostego o objętości V jest równoległobok o bokach długości a i b . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż

	1		1
2V(		+		) .
	a		b

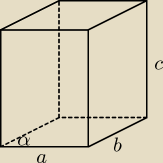Bogdan: Pole równoległoboku P = a*b*sinα ≤ a*b ponieważ dla kąta α w równoległoboku zachodzi 0 ≤ sinα ≤ 1 V = a*b*c*sinα ≤ a*b*c

	2abc		2abc
pole powierzchni bocznej PB = 2*a*c + 2*b*c =		+		=
	b		a

1

1

1

1

1

1

= 2abc(

+

) ≥ 2abcsinα(

+

) = 2V(

+

)

b

a

b

a

b

a

	1		1
czyli PB ≥ 2V(		+		) c.n.w.
	b		a