Oblicz sinusy qulla: W trójkącie ABC (równobocznym) obrano taki punkt D na odcinku BC, że BD/DC = 3/1. Oblicz sinusy kątów, na jakie został podzielony kąt CAB przez odcinek AD.

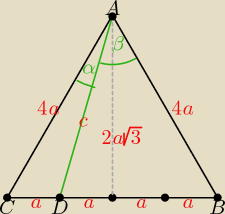
Bogdan: Kąty α i β są ostre. I sposób: c² = (2a√3)² + a² ⇒ c² = 13a² ⇒ c = a√13 Korzystając z twierdzenia kosinusów otrzymujemy: a² = (4a)² + c² − 2*4a*c*cosα ⇒ cosα = ... ⇒ sinα = √1 − cos²α (3a)² = (4a)² + c² − 2*4a*c*cosβ ⇒ cosβ = ... ⇒ sinβ = √1 − cos²β II sposób

	1		1
Pole trójkata CDA: PCDA =		*a*2a√3 oraz PCDA =		*4a*a√13*sinα
	2		2

1		1		√3
	*a*2a√3 =		*4a*a√13*sinα ⇒ sinα =
2		2		2√13

Analogicznie wyznaczyć można sinβ.

qulla: Panie Bogdanie, dziękuję Panu bardzo za pomoc z tym zadaniem!

Bogdan:

qulla: Ale dlaczego wysokość w tym trójącie równobocznym wynosi 2a√3?

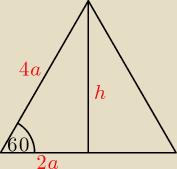
Bogdan: Z twierdzenia Pitagorasa: h = √16a² − 4a² = √12a² = 2a√3 albo

h
	= tg60o ⇒ h = 2a√3 bo tg60o = √3
2a

albo z wzoru na wysokość trójkąta równobocznego o boku długości 4a

	1
h =		*4a*√3 = 2a√3
	2

albo od razu na podstawie własności trójkąta prostokątnego o kącie ostrym 60^o h = 2a√3

qulla: O matko, panie Bogdanie, jeszcze raz bardzo dziękuję, bo właśnie tak patrzę i patrzę i przecież h w trójkącie równobocznym a√3*¹₂, ale teraz moje wątpliwości zostały całkowicie rozwiane