Romb Radziu0890: Oblicz pole rombu o boku 17 cm, w którym długość przękątnych różnią sie o 14 cm. Próbowałem to rozwiązac za pocmo twierdzenia pitagorasa ale nic nie wychodziło. [0,5 (x + 14)]² + (0,5x)² = 17² Nic mądrego nie wychodzi.

Radziu0890: Dałby ktoś rade to zacząć ?

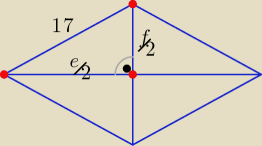
Bogdan: e, f to długości przekątnych.

	ef
Pole rombu: P =
	2

	e		f		e2		f2
(		)2 + (		)2 = 172 ⇒		+		= 289 ⇒ e2 + f2 = 4*289
	2		2		4		4

oraz

	1
e − f = 14 ⇒ (e − f)2 = 196 ⇒ e2 − 2ef + f2 = 196 ⇒ 4*289 − 2ef = 196 / *
	4

	ef
289 − 49 =		⇒ P = 240
	2

Radziu0890: e − f = 14 ⇒ (e − f)² = 196 <− tego troche nie rozumiem, skad sie to wzieło a raczej jak do tego doszłedłes ? Potem użyłes wzoru skróconego mnożenia, potem podstawiłes 4*289 za e² + f² , dalej to już tylko liczenie. Prosze o odpowiedz na moje pytanie.

Bogdan:

	ef
Wcale nie doszedłem, po prostu wiem, że potrzebne jest wyrażenie e*f, bo pole P =		,
	2

a takie wyrażenie występuje w rozwinięciu wzoru skróconego mnożenia: (e + f)² oraz (e − f)². W zadaniu narzucona jest różnica: e − f = 14, to grzech z niej nie skorzystać. Bierzemy więc tę różnicę i podnosimy obustronnie do kwadratu po to, aby wyskoczyło nam potrzebne e*f. Równość: e² + f² = 4*289 wyjaśnia rysunek.

Radziu0890: Po głębszej analizie rozumiem, dziękuje bardzo i sam nigdy bym nie doszedl do tego zeby to podnieść do kwadratu. (e − f = 14 )

Radziu0890: Jeszcze jedno pytanie, czy są inne sposby rozwiązania tego zadania ?

tim: Jest inny sposób. Podobny, ale ciut inny.

Radziu0890: Poprosze

tim: Skoro przekątne różnią się o 14, ich połowy różnią się o 7. E/2 = x F/2 = x − 7 x² + (x − 7)² = 17² x² + x² − 14x + 49 = 289 2x² − 14x = 240 /:2 x² − 7x = 120 x(x − 7) = 120 x = 15 x − 7 = 8 Zatem przekątne mają długość: e = 30 f = 16

	ef
Pole można obliczyć z wzoru
	2

Radziu0890: Ten bardziej rozumiem. x² − 7x = 120 x(x − 7) = 120 nie wiem tylko jak z tego wyszło 15

tim: A. Wypisujesz pary dzielników 120 i szukasz różniących się o 7. 15 i 8. B. Równanie kwadratowe. x² − 7x − 120 = 0

Poranny ptaszek: Pierwszego troszke nie rozumiem, (trudno sie odnaleźć po wakacjach) Drugi obliczyłem x1 i x2 i wyszło pięknie.

Poranny ptaszek: Kurde jeden wyszedł −8 a drugi 15 ..... bryyyy