Całka oznaczona z sin(x)^2 pod pierwiastkiem majk: ∫√sin(x)²dx w granicach od 0 do 2pi próbuję to rozbroić z wartości bezwzględnej, rozbijając na dwa przypadki i otrzymując = −cos(x)+C, dla sin(x)≥0 = cos(x)+C, dla sin(x)<0 przy czym, podstawiając granice całkowania otrzymuje: (−1−(−1))=0 co według mojego zbioru i wolframa jest błędne http://www.wolframalpha.com/input/?i=integrate+sqrt%28sin%28x%29%5E2%29+from+0+to+2pi co robię źle?

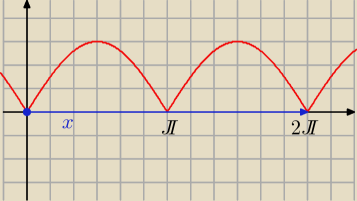
Trivial: ∫₀^2π|sinx|dx = 2*∫₀^π|sinx|dx = 2*∫₀^πsinxdx = 2*[−cosx]₀^π = −2*(−1−1) = 4.

Trivial: A rozbijając z wartości bezwzględnej też powinno wyjść. ∫₀^2π|sinx|dx = ∫₀^πsinxdx + ∫_π^2π(−sinx)dx = [−cosx]₀^π + [cosx]_π^2π = (1+1) + (1−(−1)) = 4.

majk: super, zrozumiałem gdzie był mój błąd rozumowania. wielkie dzięki!