trójkąt prostokątny, ciąg nie_mam: Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny o różnicy r>0. Oblicz długość promienia okręgu wpisanego w ten trójkąt. Ja zrobiłam to tak: Oznaczyłam boki jako x, x+r, x+2r Dalej liczyłam z twierdzenia Pitagorasa: x²+(x+r)² = (x+2r)² Z tego wyszło: x² + 2rx − 3r² = 0 x₁/x₂= r/−3r Skoro r>0 to x₂ odpada. Więc wychodzi, że bok jest równy r, drugi 2r, a trzeci 3r. I teraz chciałam policzyć długość promienia ze wzoru

	2P
R=
	a+b+c

	r
Wychodzi mi		, a w odpowiedziach jest r.
	6

Co robię źle?

zośka: Tam powinno być : x²−2xr−3r²=0 x₁=−r (odpada) , x₂=3r boki: 3r,4r,5r

zośka: Masz policzyć ponadto promień okręgu wpisanego! Niech R − promień okręgu wpisanego w trójkąt

	3r*4r
PΔ=		=6r2
	2

z drugiej strony:

	1		1		1		1
PΔ=		3r*R+		4r*R+		5r*R=		12r*R=6r*R
	2		2		2		2

Porównując oba wzory dostajemy, że musi by R=r

zośka: Tam oczywiście ma być:

	1		1		1
PΔ=		*3r*R+		*4r*R+		*5r*R,
	2		2		2

zośka: Przepraszam, wzór masz na R ok. A błąd wynikał z błędu rachunkowego: x²+2xr−3r²=0 zamiast x²−2xr−3r²=0

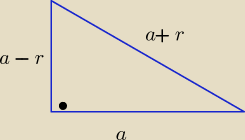
Eta: r−−− różnica ciągu arytmetycznego , r>0 i a>0

	a+b−c		a−r+a −a−r		a
Rw=		=		=		−r
	2		2		2

(a−r)²+a²=(a+r)² a²−4ar=0⇒ a(a−4r)=0 ⇒ a= 4r

	4r
Rw=		−r= r
	2