 Mam problem z takim zadaniem:
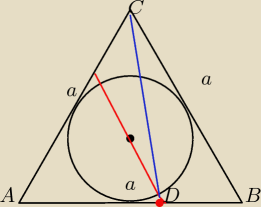
Przez środek okręgu wpisanego w trójkąt równoboczny ABC poprowadzono prostą równoległą do boku
BC i przecinającą bok AB w punkcie D. Oblicz iloraz |DC|/|DB| .
Bardzo proszę o pomoc.
Mam problem z takim zadaniem:
Przez środek okręgu wpisanego w trójkąt równoboczny ABC poprowadzono prostą równoległą do boku
BC i przecinającą bok AB w punkcie D. Oblicz iloraz |DC|/|DB| .
Bardzo proszę o pomoc.

 nie wiem czy dobrze, więc
nie wiem czy dobrze, więc 
| 2 | 2 | |||
Punkt O jest odległy od wierzchołka A o R= | h= | *U{a√3{2}=U{a√3{3} | ||
| 3 | 3 |
| 2 | a | |||
|AD|= | a, |DB|= | |||
| 3 | 3 |
| 2 | 2 | |||
|CD|2=a2+( | a)2−2a* | a*cos600 | ||
| 3 | 3 |
| 4 | 2 | 1 | ||||
|CD|2=a2+ | a2−2a* | a* | ||||
| 9 | 3 | 2 |
| 13 | 2 | 7 | ||||
|CD|2= | a2− | a2= | a2 | |||
| 9 | 3 | 9 |
| a√7 | ||
|CD|= | ||
| 3 |
| |CD| | a√7 | a | |||
= | : | =√7 | |||
| |DB| | 3 | 3 |
 Wszystko rozumiem, oprócz jednego, aczkolwiek ważnego punktu, mianowicie
czemu |AD|=2/3a, skąd to wiadomo? Wiem, że trójkąty są podobne, szukałam drogi jaką szłaś
sporo czasu, ale nie widzę związku.
Wszystko rozumiem, oprócz jednego, aczkolwiek ważnego punktu, mianowicie
czemu |AD|=2/3a, skąd to wiadomo? Wiem, że trójkąty są podobne, szukałam drogi jaką szłaś
sporo czasu, ale nie widzę związku.
| 2 | 2 | |||
|AO|=R= | hΔ jest wysokością w odciętym Δ ,stosunek wysokości jest równy | i to jest | ||
| 3 | 3 |
 Dziękuję jeszcze raz
Dziękuję jeszcze raz 
