matura próbna janusz: witam, rozwiązuję zadania z tego zestawu i chciałbym znać do nich rozwiązania, żeby wiedzieć czy moje wyniki są prawidłowe. z góry dziękuję za odpowiedzi Zadanie 1 (4 pkt.) Wyznacz zbiór wartości funkcji 2 f(x) = x + | logx 201 3|⋅log2013x . Zadanie 2 (5 pkt.) Rozwiąż nierówność x6 + 2x5 − 3x4 − 8x3 + 8x + 4 ≤ 0. Zadanie 3 (4 pkt.) Oblicz pole trapezu ABCD , którego podstawy mają długości |AB | = 11 i |CD | = 5 , a ramiona mają długości |AD | = 3 i |BC | = 6 . Zadanie 4 (4 pkt.) Rozwiąż równanie ( ) ( ) cos2 π6 + x + cos2 π6−− x = 12 + cosx . Zadanie 5 (6 pkt.) W trójkącie prostokątnym ABC przyprostokątne mają długości √ −−− |BC | = 8 , |CA | = 17 . Na boku AB wybrano punkt D tak, że |AD | = 2 . Oblicz sinus kąta DCA . Zadanie 6 (4 pkt.) Dane są liczby a,b,c ∈ R takie, że równanie 4 2 ax + bx + c = 0 ma cztery rozwiązania rzeczywiste x1,x2,x3,x4 . Oblicz wartość wyrażenia |x1|+ |x2|+ |x 3|+ |x4| . Zadanie 7 (4 pkt.) Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 27, a iloczyn drugiej i trzeciej jest równy 72. Wyznacz te liczby Zadanie 8 (6 pkt.) Wielomian 4 3 2 W (x) = 6x + 10x + ax − 1 5x+ b jest podzielny przez trójmian P (x) = 3x 2 + 5x − 7 . Wyznacz liczby a i b . Zadanie 9 (4 pkt.) Oblicz prawdopodobieństwo, że w dziesięciu rzutach kostką dokładnie na dwóch kostkach otrzymamy ściankę z dwoma oczkami i dokładnie na trzech kostkach ściankę z trzema oczkami. Zadanie 10 (5 pkt.) Pole równoległoboku ABCD o danych wierzchołkach A = (5,2) i B = (4,− 1) jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej y = −x + 10 , który ma obie współrzędne będące liczbami całkowitymi. Zadanie 11 (4 pkt.) Oblicz odległość środka ściany sześcianu o krawędzi długości a od przekątnej tego sześcianu.

janusz: widzę, że niektóre źle się skopiowały Zadanie 2 wygląda tak x⁶ + 2x⁵ − 3x⁴ − 8x³ + 8x +4 = 0 Zadanie 4 cos²(π/6 + x) + cos²(π/6 − x) = 1/2 + cos x Zadanie 5 BC = 8 CA = √17 zadanie 6 ax⁴ + bx² + c = 0 zadanie 8 6x⁴ + 10x³ + ax² − 15x + b jest podzielny przez trójmian 3x² + 5x + 7

krystek: Ale Ty masz umieć , wyliczaj , poprawimy!

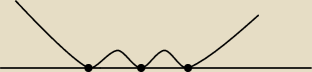
janusz: dobra to podam to, co na chwile obecną mam zadanie 1. x>0 z założeń, zatem |logx2013| = logx2013 x² + logx2013 * log2013x = x² + 1 ZW: <1:∞) zadanie 2. x6 + 2x5 − 3x4 − 8x3 + 8x +4 ≤0 (x+1)² * [(x−√2)(x+√2)≤0 x≤0 dla x∊{−√2, +√2, −1}| zadanie 3. cos2(π/6 + x) + cos2(π/6 − x) = 1/2 + cos x cos(π/6 + x) * cos(π/6 + x) + cos(π/6 − x) * cos(π/6 − x) = 1/2 + cosx cos π/6 = √3/2 dla lewej strony stosuję funkcję sumy i różnicy kątów i wyszło mi że równa się zero 0 = 1/2 + cosx cosx = −1/2 cosx ∊ (2/3π + 2kπ; 4/3π + 2kπ}

janusz: zadanie 4 znalazłem juz w necie i zgadza się z moim rozwiązaniem: sinα=16/33

FiFi: czemu I logx2013 I=logx2013 Przecież za x moge podstawić np:1/2 i wtedy pod wartoscia bezwzględna mam liczbe ujemna, czyli I logx2013 I= − logx2013