Prośba o sprawdzenie zadania temporary: Miara kąta między ramionami trójkąta równoramiennego o polu P jest równa α. Oblicz promień okręgu wpisanego w ten trójkąt. Dobrze to jest zrobione? http://ifotos.pl/zobacz/CameraZOO_nhrxeha.jpg/ Jeżeli nie prosze o wskazanie błędu.

temporary: up

Saizou :

	1
P=		a*a*sinx
	2

	2P
a2=
	sinx

	2P
a=√
	sinx

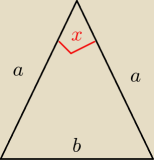
z tw. cosinusów b²=a²+a²−2a*a*cosx

	2P		2P		2P
b2=		+		−2*		*cosx
	sinx		sinx		sinx

	4P		4Pcosx
b2=		−
	sinx		sinx

	4P−4Pcosx
b2=
	sinx

	P−Pcosx
b=2√
	sinx

	2P
r=
	a+a+b

	2P
r=
	2P   P−Pcosx   2√ +2√   sinx   sinx

	P
r=
	2P   P−Pcosx   √ +√   sinx   sinx

Mila: Doprowadzić do postaci:

	√Psinα
r=
	α   √2*(1+sin )   2

temporary: @Saizou masz tak jak ja, czyli chyba zrobiłem dobrze. Pytałem sie z ciekawości bo na zadania.info jest wynik bodajże ten, co kolega/koleżanka @Mila podał/a i nie wiedziałem czy to to samo bo nie potrafiłęm przekształcić

Mila: To samo, właśnie z Twojego wyniku to otrzymałam.

temporary: Mogła byś mi pokazać po kolei przekształcenia?

Mila: Piszę.

Mila:

	2√2p		√4P*(1−cosα)
Mianownik:{		+		=
	√sinα		√sinα

	2√2P+2√P*(1−cosα)
=		=
	√sinα

	2√P*√2+2√P*√1−cos2(α/2)+sin2(α/2)
=		=
	√sinα

	2√P*(√2+√2sin2(α/2))
=		=
	√sinα)

	2√P*(√2+√2sin(α/2))		2√P*√2*(1+sin(α/2))
=		=
	√sinα)		√sinα

	2P
r=		=
	2√P*√2*(1+sin(α/2))   √sinα

2P*√sinα		√Psinα
	=
2√P*√2*(1+sin(α/2))		α   √2*(1+sin )   2