. asdf: Witam, metoda Monte Carlo. No i mam tak.. Określam najmniejszą wartość: y_min = 1 y_max = 2 x_min = 1 x_max} = 2 Losuje sobie, np. N= 1000 punktów (x_i,y_i) gdze x_i ∊ (1,2), y_i ∊ (1,2) robię zmienną k=0; i sprawdzam czy punkt ten leży pod osią, czyli, czy: y_i < f(x_i) jeżeli tak to k=k+1; Końcowy wynik to V = (x_max − x_min)*(y_max − y_min) * k/N, czyli inaczej: S = niebieska kreska * zielona kreska V = S * k/N; i wychodzi mi w całce: ∫₀¹ x dx ≈ 0.51 .... a powinno wyjść 3/2. Za y_min powinienem dać wartość 0? czy jak?

asdf: ?

asdf: ?

xx:

	1
∫01 x dx =		x2 |01 = 1/2
	2

aniabb: żeby w całce wyszło 3/2 to trzeba całkować od 1 do 2 bo taki masz zakres x jeśli się ograniczasz do y>1 to od całki musisz odjąć prostokąt Δx•y tu =1 jeśli na Ci wyjść w losowaniu 3/2 to losować musisz od y=0

Trivial: Trzeba zrobić tak, żeby funkcja przyjmowała wartości y ∊ [0,c], c>0 Chcemy całkować f(x) w przedziale x ∊ [a,b]. Określamy y_min, y_max, tak jak to zrobiłeś. Przesuwamy funkcję tak, aby przyjmowała wartości y∊[0,c], (c = y_max−y_min) czyli: f*(x) = f(x) − y_min → f(x) = f*(x) + y_min Całkujemy i mamy: ∫_a^b f(x)dx = ∫_a^b (f*(x) + y_min)dx = ∫_a^b f*(x)dx + y_min(b−a) = p*S + y_min(b−a) Gdzie S oznacza pole prostokąta, w którym całkujemy S = (y_max−y_min)(b−a) W Twoim przykładzie: S = (2−1)*(2−1) = 1 p = 0.5 ∫₁² xdx = p*S + y_min(b−a) = 0.5*1 + 1*(2−1) = 1.5

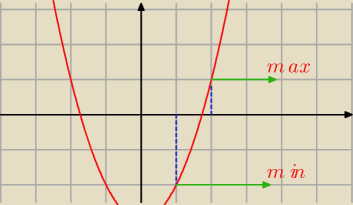
asdf: dzieki za odpowiedź, już na to wpadlem na zajęciach i jakoś wyszło żeby zliczać k (licznik) to chyba jeszcze trzeba dać taki warunek: y_min*y_max < 0 − wtedy liczy się normalnie pole V= (ymax −ymin)*(xmax − xmin) * k/N k − licznik N − ilość tych prób

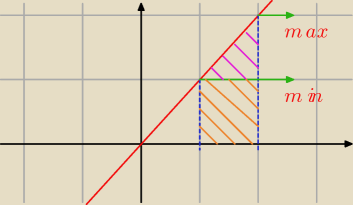
asdf: dla funkcji, gdzie y_min ≠ 0 i y_min ma taki sam znak to chyba trzeba użyc takiego czegos: jeżeli y_min * y_max > 0 (te same znaki) oraz y_min ≠ 0 to licz pole w taki sposob: V = (ymax − ymin)*(xmax − xmin) * k/ N + |y_min|*(xmax − xmin) dobrze?

aniabb: na pole pod krzywą ..pasuje

asdf: nad krzywą (dla wartosci ujemnych tylko inaczej zliczać + warunek dodatkowy na te przypadki

aniabb: albo przesunąć wykres czyli jak ymin <0 to dodawać go do wyników Losuje sobie, np. N= 1000 punktów (xi,yi) gdze xi ∊ (1,2), yi ∊ (0,2) robię zmienną k=0; i sprawdzam czy punkt ten leży pod osią, czyli, czy: yi < f(xi)+ymin jeżeli tak to k=k+1;

aniabb: wtedy zawsze od ymin =0 i nie musisz dodawać pola albo dzielić na przedziały

aniabb: jadę ..będę jutro rano ..albo może zajrzę wieczorkiem

Bogdan: Jako ciekawostkę podam, że metodę Monte Carlo opracował jeden z najwybitniejszych matematyków XX wieku − Stanisław Ulam. Jest polskim uczonym pracującym przez większą część życia w USA. Jest m.in. współautorem pierwszej bomby atomowej. Przez wiele lat jego osoba i osiągnięcia nie były w Polsce szeroko przedstawiane. http://pl.wikipedia.org/wiki/Stanis%C5%82aw_Ulam http://www.matematycy.interklasa.pl/biografie/matematyk.php?str=ulam

asdf: dziękuje bardzo Przy Was idzie się dużo nauczyć

asdf: @aniabb, to chyba nie działa

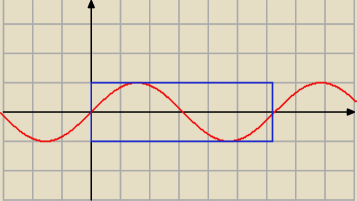
Trivial: Kilka przykładów: ∫_a^b f(x) dx = p*S + y_min*(b−a) ∫₀^2π sin(x) dx = 0.5*(1+1)*2π − 1*2π = 2π − 2π = 0.

aniabb: a jakie dokładnie jest polecenie?

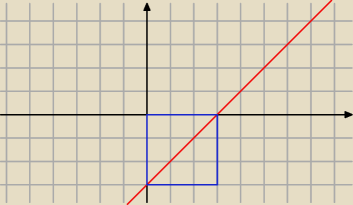
Trivial: ∫₀³(x−3)dx = 0.5*3² − 3*3 = − 4.5

asdf: @aniabb polecenie − liczenie całki oznaczonej metodą monte carlo @trivial ale to z: p*S + ymin*(b−a) dajmy ymin = −3, ymax = 4, wtedy liczysz w tym polu co trzeba (nie unikasz sytuacji, ze pomijasz jakiś prostokąt − wiec nie trzeba dodawać ymin*(b−a) chyba..

aniabb: no to tak jak pisze trivial i jak napisałeś sam o 14:30 wzór będzie ∫_a^b f(x) dx = p*S + y_min*(b−a) jak rozciągniesz za bardzo w dół y_min to trzeba będzie go odjąć (co załatwi sam znak y) jak będzie za wysoko to dodać (j.w.)