Geo analityczna Rozszerzenie parzon: W czworokącie ABCD przekątne AC i BD przecinają się w punkcie S(4,4) i dzielą się tak, że |SB| = |SD| = 2√5 oraz |AC| = 3|SC|. Przekątna BD zawiera się w prostej o równaniu x + 2y −12 = 0, zaś A(−2,−8) a) wyznacz współrzędne pozostałych wierzchołków b) oblicz pole czworokąta.

Aga1.:

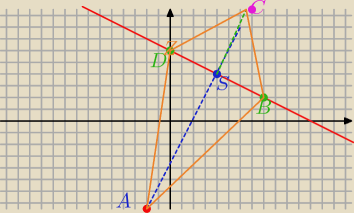
	−1		−1
B(x,		x+6), B lezy na prostej y=		x+6)
	2		2

	1
ISBI=√(x−4)2+(−		x+2)2=2√5
	2

Otrzymasz dwa rozwiązania (0,6) lub (8,2) C wyliczysz z wektorów AC→=3*SC→ [x+2,y+8]=3[x−4,y−4] x+2=3x−12, y+8=3y−12 C(7,10) b)Zastosuj wzór na pole deltoidu.( przekątne obliczysz ze wzoru na długość odcinka)