Wyznacz liczbę rozwiązań równania w zależności od parametru a Daniela: |||x−2|−2|−2|=|a−2|−2

Edek: a (0,4) − brak rozwiązań a {0,4} − 3 rozwiązania a (−∞,0) u (4,+∞) − 6 rozwiązań ( lub 8 ) ?

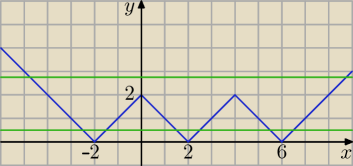
Bogdan: y = |||x − 2| − 2| − 2| (niebieska linia) Wykres y = |a − 2| − 2 (zielona linia) jest wykresem funkcji stałej i może przyjmować różne położenia w zależności od parametru a. Np.: jeśli |a − 2| − 2 > 2 to a∊(−∞, −2)∪(6, +∞), zielona linia przecina niebieską w dwóch punktach, więc równanie |||x − 2| − 2| − 2| = |a − 2| − 2 dla a∊(−∞, −2)∪(6, +∞) ma 2 rozwiązania. Edku, Twoje rozwiązanie trzeba poprawić i uzupełnić.