pomoze ktos , prosze :* ? Martaaa95: 1.Graniastosłup prawidłowy sześciokątny ma pole boczne równe polu podstawy. jaka jest objętość, jeżeli krawędź podstawy ma długość 5. 2. Ostrosłup prawidłowy czworokątny przecięto płaszczyzna przechodzącą przez przeciwległe krawędzie ścian bocznych. Otrzymany przekrój jest trójkątem prostokątnym. Jakie jest pole i objetość ostrosłupa, jeżeli krawędź podstawy ma długość 3√2 ?

Mila: 1) Skorzystaj z rysunku do zadania z graniastosłupem sześciokątnym. Pole podstawy: a=5 dł. boku sześciokąta

	a2√3		52√3		25√3		75√3
P=6*		=6*		=3*		=
	4		4		2		2

P_b=6*a*H H− wysokość graniastosłupa

	75√3
6*5*H=		/:5
	2

	15√3
6H=
	2

	5√3
H=
	4

	75√3		5√3		75*5*3
V=Pp*H=		*		=		wymnóż
	2		4		8

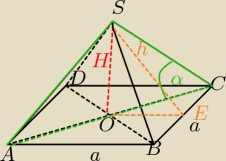
Mila: ΔACS− Δprostokątny równoramienny,⇒α=45⁰ |SO|=H=|OC| a=3√2 AC=a√2=3√2*√2=6 H=3

	1
V=		a2*H
	3

	1
V=		*(3√2)2*3=9*2=18
	3

V=18j³

	1
Pc=a2+4*		a*h
	2

h²=H²+OE² h²=3²+(1,5√2)² h²=9+2,25*2

	27
h2=9+4,5=13,5=
	2

	3√3
h=
	√2

	3√6
h=
	2

	3√6
Pc=(3√2)2+2*3√2*		=9*2+3√2*3√6
	2

P_c=18+9√12=9*(2+√12) P_c=9*(2+2√3)=18(1+√3)

Martaaa95: danke .